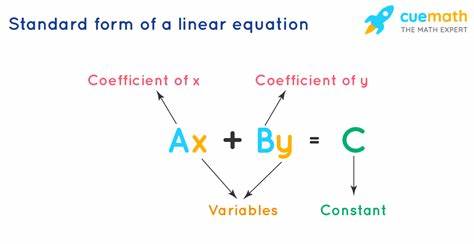
Линейные уравнения занимают важное место в математике и её приложениях. Эти уравнения, графики которых образуют прямые линии, используются в физике, экономике, инженерии и многих других науках. Одной из самых удобных и часто применяемых форм записи линейных уравнений является стандартная форма. Понимание, что такое стандартная форма линейного уравнения и как её использовать, помогает в решении множества задач, связанных с графиками, системами уравнений и моделированием. Стандартная форма линейного уравнения выглядит так: Ax + By = C, где A, B и C — числовые коэффициенты, которые могут принимать значения как положительные, так и отрицательные, включая ноль.
При этом буквы x и y обозначают переменные, координаты точек на плоскости. Примеры таких уравнений могут быть разными. Например, уравнение 3x + 7y = 10 – это классический случай, где коэффициенты A = 3, B = 7 и C = 10. В другом варианте может быть уравнение x + 5y = 6, где A равен 1, а переменная x обозначена просто единицей, что реализуется при записи без явного коэффициента. Также иногда встречаются уравнения типа 8y = 9, где коэффициент при x отсутствует, что равносильно тому, что его значение равно нулю.
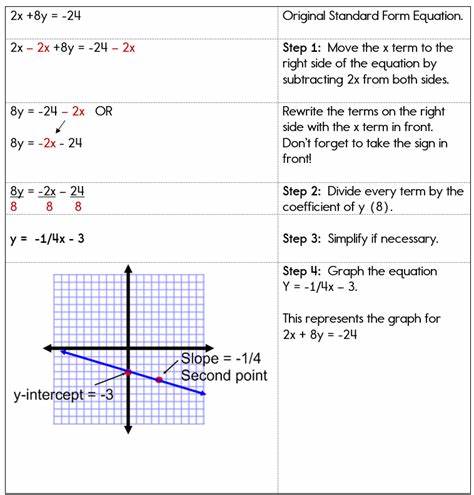
Очень важно понимать, что в стандартной форме могут появляться и отрицательные коэффициенты, например, уравнение 3x − 5y = 12. Здесь B равно −5, и такое уравнение вполне корректно и широко применяется. Одним из основных преимуществ записи уравнения в стандартной форме является удобство нахождения точек пересечения графика с осями координат, или, говоря иначе, нахождение x- и y-перехватов. Для x-перехвата достаточно приравнять y к нулю и найти соответствующее значение x. Аналогично, для y-перехвата приравнивают x к нулю и определяют y.
Такой способ позволяе быстро и просто найти ключевые точки линии на графике. Более того, стандартная форма часто используется, когда речь идёт о системах линейных уравнений. При решении задач на пересечение двух или более прямых, удобнее всего иметь их уравнения в одном формате, в частности, стандартном. Это позволяет применять метод подстановки, сложения или вычитания уравнений с максимальной эффективностью и минимальной вероятностью ошибок. Часто возникает необходимость преобразовать уравнение из других форм в стандартную.
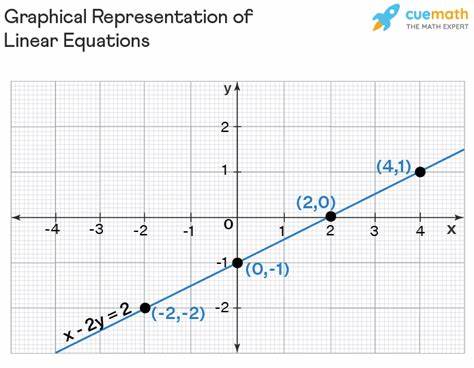
Наиболее популярными альтернативными формами являются уравнение с угловым коэффициентом и точкой (точка-наклон) и уравнение с наклоном и y-перехватом (угловое с y-перехватом). Чтобы конвертировать уравнение в стандартную форму, важно привести все члены уравнения в такой вид, чтобы с одной стороны были все члены с переменными, а с другой – свободный член-константа. Рассмотрим пример, когда известны две точки на плоскости, и требуется составить уравнение прямой в стандартной форме. Предположим, у нас есть точки (1, 1) и (2, 3). Вначале вычисляем наклон (угловой коэффициент) линии, используя изменение по y, делённое на изменение по x, то есть (3-1)/(2-1) = 2.
Имея наклон, можно подставить одно из значений точки и использовать точечную форму уравнения прямой y–y1 = m(x–x1), которая в нашем случае выглядит как y – 1 = 2(x – 1). Раскрыв скобки и преобразовав уравнение, получаем y – 1 = 2x – 2, откуда y = 2x – 1. Это уравнение уже записано в популярной форме y = mx + b, где m – наклон, а b – y-перехват. Чтобы перейти к стандартной форме, нужно убрать переменные с одной стороны уравнения и выровнять коэффициенты. Для этого можно вычесть 2x из обеих частей: y – 2x = –1 или, переставив слагаемые, −2x + y = −1.
Таким образом, коэффициенты A = −2, B = 1 и C = −1, и уравнение запишется как −2x + y = −1. Для более удобного и традиционного вида можно умножить обе части на −1, получив 2x − y = 1. В конечном итоге, освоение стандартной формы линейного уравнения и навыков преобразования других форм существенно облегчает работу со множеством математических задач. Это позволяет быстро переходить от аналитического описания прямой к её графическому изображению и обратно. Кроме этого, стандартная форма упрощает изучение систем уравнений, особенно когда они имеют различные формы и требуют приведения к общему знаменателю для нахождения точек пересечения.