Линейные уравнения — один из фундаментальных элементов алгебры, широко применяемый в математике, физике, экономике и многих других областях. Среди различных способов представления линейных уравнений особое место занимает стандартная форма, которая обеспечивает удобство при решении систем уравнений и построении графиков. Понимание стандартной формы является важным этапом в овладении математическими навыками, необходимыми как для школьников, так и для студентов. В данной статье рассмотрим, что такое стандартная форма линейного уравнения, какие преимущества она представляет, а также подробно ознакомимся с процессом преобразования и графическим изображением таких уравнений на плоскости. В завершение приведем конкретные практические примеры для закрепления материала.
Стандартная форма линейного уравнения — это выражение уравнения, нацеленное на ясное представление взаимосвязи между переменными. Для уравнений с одной переменной она выглядит как Ax + B = 0, где A и B — целые числа, а переменная x — неизвестная. Такие уравнения позволяют быстро находить значение переменной и решать задачи, связанные с прямолинейным графиком на координатной оси. В более общем случае, когда уравнение содержит две переменные, используется форма Ax + By = C, где A, B и C — целые числа, а A положительно и не равен нулю. Переменные x и y — координаты на плоскости, что позволяет представить уравнение графически в виде прямой линии.
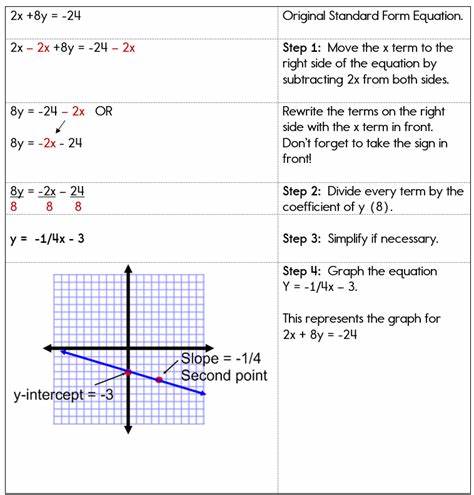
Формат Ax + By = C важен тем, что дает структурированное и упрощенное представление, удобное для решения систем уравнений, анализа пересечений линий и вычисления точек пересечения с осями координат. Одним из главных достоинств стандартной формы является легкость преобразования из других, более распространенных видов уравнений, таких как наклонно-перехватная (y = mx + b) или точечно-наклонная форма (y - y1 = m(x - x1)). Например, если уравнение задано в наклонно-перехватной форме, можно без труда привести его к стандартной, что значительно облегчает последующую работу с уравнением, особенно при построении графиков. Рассмотрим на практике преобразование уравнения y = (2/3)x - 4. Для избавления от дроби умножим обе части уравнения на 3, получив 3y = 2x - 12.
Далее соберем все переменные с одной стороны: 3y - 2x = -12. Так как коэффициент при x отрицательный, умножим на -1, чтобы получить 2x - 3y = 12 — стандартную форму нашего уравнения. Аналогичный подход применяется при работе с точечно-наклонной формой. Например, исходное уравнение y - 4 = 1/2(x - 6) умножаем обе части на 2, что дает 2(y - 4) = x - 6. Раскрываем скобки, 2y - 8 = x - 6.
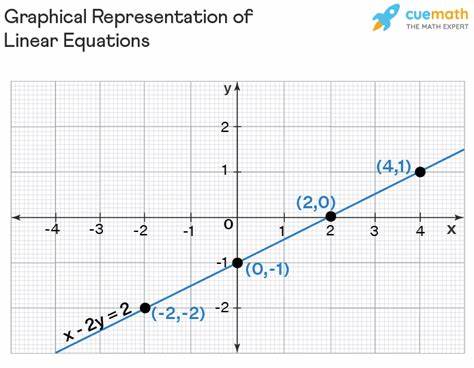
Корректируем уравнение, перемещая x в левую часть и числа в правую: 2y - x = 2. Так как коэффициент при x отрицательный, умножаем на -1 и получаем x - 2y = -2 — стандартную форму уравнения. Овладев навыками преобразования, легко перейти к графическому представлению линейных уравнений. Стандартная форма помогает определить точки пересечения с осями координат — важные опорные точки для построения прямой линии на плоскости. Для нахождения x-пересечения подставляем y = 0 и решаем уравнение относительно x, а для y-пересечения — наоборот, подставляем x = 0 и находи y.
Рассмотрим пример 4x + 3y = 12. При y=0 уравнение превращается в 4x = 12, давая x = 3, значит x-пересечение в точке (3, 0). Аналогично, при x=0, 3y = 12, откуда y = 4, и y-пересечение окажется в пункте (0, 4). Эти две точки позволяют без труда построить прямую линию. Использование стандартной формы упрощает решения задач, связанных с системами линейных уравнений, когда необходимо определить точку пересечения двух или более прямых.
Поскольку уравнения удобно расположены, их можно подставлять друг в друга или применять методы сложения и вычитания для нахождения неизвестных. На практике большое значение имеет также четкое понимание того, как линейное уравнение можно перейти от одной формы к другой. Например, зная наклон и точку пересечения, можно преобразовать уравнение в стандартную форму, что особенно полезно при аналитических вычислениях и в программировании. Например, для прямой с наклоном 3/4 и y-пересечением -2 исходное уравнение в наклонно-перехватной форме y = (3/4)x - 2 можно умножить на 4, что дает 4y = 3x - 8, затем привести к виду -3x + 4y = -8 и, домножив на -1, получить 3x - 4y = 8 — желаемую стандартную форму. Данная форма позволит легко находить пересечения и свойства линии.
Практические примеры служат отличным способом закрепления знаний, особенно для учеников и преподавателей. Рассмотрев уравнение y = (5/2)x - (7/3), для упрощения выражаем правую часть с общим знаменателем: y = (15/6)x - (14/6), дальше умножаем обе части на 6, получая 6y = 15x - 14, собираем члены в стандартный вид: -15x + 6y = -14, и, умножая на -1, в итоговую 15x - 6y = 14. Такой порядок действий удобен и универсален для любых дробных коэффициентов. На практике при изучении стандартной формы линейных уравнений важно развивать умение быстро преобразовывать, находить перехваты и строить графики, потому что они — основа многих последующих тем по алгебре и аналитической геометрии. Уверенное владение этой темой помогает при решении сложных задач на системы уравнений, оптимизацию и даже в программной реализации математических моделей.
В заключение стоит отметить, что стандартная форма линейного уравнения — это не только способ хранения уравнения в удобном формате. Это мощный инструмент для анализа, визуализации и решения точки пересечения и взаимосвязи переменных. Знание процесса перехода из одной формы в другую расширяет математический кругозор и упрощает освоение более сложных математических концепций. Осваивая эту тему, школьники и студенты получают фундамент для успешного изучения алгебры и геометрии, уверенно решая практические задачи и развивая аналитическое мышление.