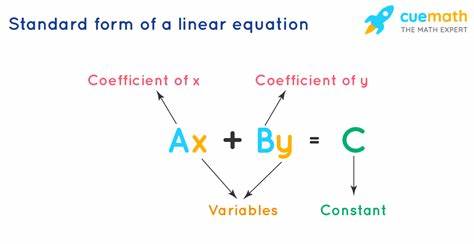
Линейные уравнения занимают ключевое место в алгебре и математике в целом. Они являются основой для решения различных задач, связанных с прямыми линиями на графиках и взаимодействием переменных. Одним из самых удобных и широко используемых способов записи линейных уравнений является стандартная форма. Понимание и умение работать с этой формой существенно облегчает анализ уравнений и позволяет быстро находить важные характеристики линии, такие как точки пересечения с осями координат. Стандартная форма линейного уравнения в двух переменных записывается как Ax + By = C, где A, B и C — постоянные числа, обычно целые, а x и y — переменные.
Важное условие: коэффициенты A и B не должны одновременно равняться нулю, так как в таком случае уравнение перестаёт описывать прямую. Одним из главных преимуществ стандартной формы является её универсальность и простота преобразований. В отличие от других форм записи, таких как уравнение с угловым коэффициентом (y = mx + b), где прямая выражена через наклон и сдвиг, стандартная форма не предполагает прямого определения наклона, но зато удобна для работы с интерцептами. Интерцепты — это точки пересечения графика с осями координат, которые играют важную роль при построении графиков и физических интерпретациях. При записи уравнения в стандартной форме очень легко определить x-пересечение и y-пересечение.
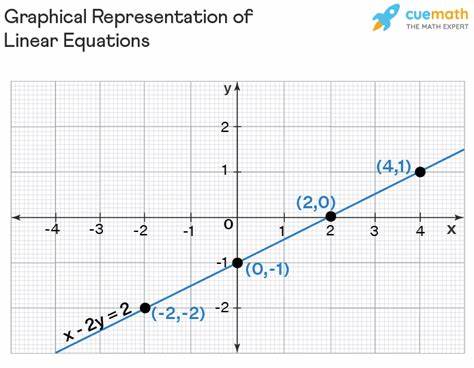
Чтобы найти x-пересечение, необходимо приравнять y к нулю и решить уравнение относительно x. Аналогично, для определения y-пересечения нужно приравнять x к нулю и найти значение y. Такой подход удобен для быстрого и точного построения графиков без использования сложных вычислений. Рассмотрим пример. Пусть дана стандартная форма уравнения 3x + 4y = 12.
Чтобы определить x-пересечение, ставим y = 0 и получаем 3x = 12, значит x = 4. Для y-пересечения при x = 0 имеем 4y = 12, то есть y = 3. Таким образом, график этой прямой пересекает ось X в точке (4, 0) и ось Y в точке (0, 3). Это позволяет быстро построить график, соединив эти две точки. Стандартная форма полезна также при решении систем линейных уравнений.
Благодаря общему виду легко организовать и упрощать уравнения, используя методы замены, сложения или вычитания. Важно отметить, что коэффициенты A и B желательно выбирать так, чтобы они были без дробных значений, что облегчает вычисления и повышает читаемость уравнения. Кроме того, стандартная форма используется в различных областях математики, физики, геометрии и инженерии. Например, при описании границ регионов на плоскости, расчёте пересечений линий или анализе физических процессов, связанных с линейными зависимостями переменных. Трансформация уравнения из одной формы в другую — важный навык.
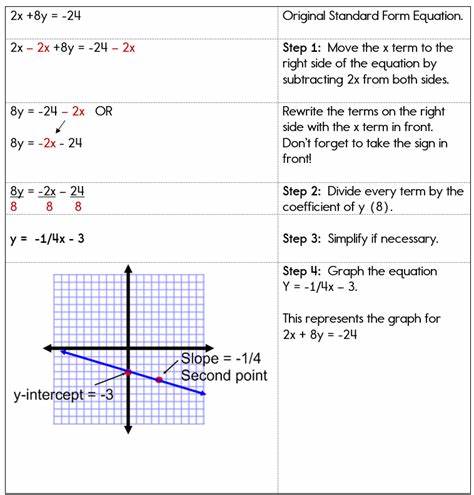
Например, уравнение в виде y = mx + b можно преобразовать в стандартную форму, перенесши все члены на одну сторону и умножив на подходящий коэффициент для избавления от дробей. Такой навык особенно полезен при подготовке к экзаменам и работе с различными типами задач, где требуется гибкое и быстрое преобразование уравнений в удобные для анализа формы. При работе с линейными уравнениями, записанными в стандартной форме, также важно понимать влияние коэффициентов на наклон и положение прямой. Коэффициенты A и B связаны с наклоном y, который равен -A/B. Это равенство помогает определить направление наклона линии, а также понять, параллельна ли прямая каким-то осам или другим линиям.