Линейные уравнения занимают важное место в математике и приложениях, связанных с анализом данных, инженерией, экономикой и многими другими областями. Под линейным уравнением понимают уравнение первого порядка, которое описывает прямую линию на координатной плоскости. Одной из самых распространённых форм представления таких уравнений является стандартная форма. В данной статье мы подробно рассмотрим, что представляет собой линейное уравнение в стандартной форме, как его распознать, решить и применить на практике. Понимание стандартной формы линейного уравнения начинается с изучения его общего вида.
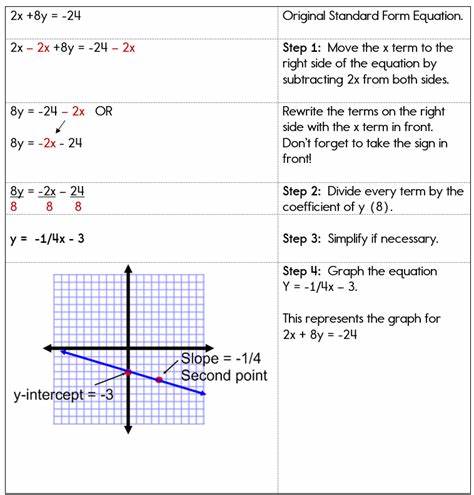
Стандартная форма обычно записывается как Ax + By = C, где A, B и C — это числовые коэффициенты, а x и y — переменные. Важно отметить, что коэффициенты A и B не равны одновременно нулю, иначе уравнение потеряет смысл. Такая форма удобна тем, что она выражает уравнение прямой без необходимости сразу преобразовывать его в другие формы, например, в уравнение с угловым коэффициентом. Коэффициенты A и B определяют наклон и ориентацию прямой, а величина C влияет на положение этой прямой на координатной плоскости. Если рассмотреть уравнение более подробно, то можно получить представление о том, как изменение одного из коэффициентов меняет расположение линии.
Это имеет важное значение при моделировании различных процессов и явлений. Преобразование различных уравнений в стандартную форму является полезным навыком. Например, уравнение в виде y = mx + b можно переписать, перенеся все члены в одну сторону, получая Ax + By = C. Для этого достаточно вычесть y с одной стороны и получить уравнение: -mx + y = b, где коэффициенты A и B принимают значения -m и 1 соответственно, а C равняется b. Такое преобразование облегчает анализ и дает возможность применять более универсальные методы работы с линейными уравнениями.
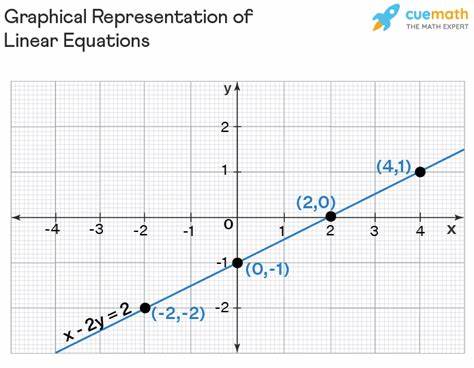
Решение линейных уравнений в стандартной форме требует использования разных методов. Один из самых эффективных подходов — это метод подстановки или метод сложения (вычитания), особенно при работе с системами уравнений. При решении одного уравнения с двумя переменными задача сводится к нахождению множества пар (x, y), которые удовлетворяют уравнению, то есть координат точек прямой на графике. Графическое представление играет важную роль в понимании линейных уравнений. Для построения прямой, заданной уравнением в стандартной форме, достаточно найти хотя бы две точки, которые удовлетворяют уравнению, и соединить их линией.
Обычно удобнее выбирать точки, где одна из переменных равна нулю, чтобы упростить вычисления. Например, при x=0 можно найти y, а при y=0 — x. Это позволяет легко построить график и визуально оценить свойства линии. Линейные уравнения в стандартной форме широко применяются в самых разных сферах. В экономике они помогают моделировать зависимости между затратами и доходами, в физике — описывать линейные процессы, а в технике — рассчитывать параметры систем.
Способность быстро переводить уравнение в стандартную форму и решать его расширяет возможности специалистов и учащихся, позволяя точнее анализировать информацию. В образовательном процессе изучение линейных уравнений способствует развитию аналитического мышления и умению работать с абстрактными понятиями. Умение не только решать такие уравнения, но и понимать их геометрическое и практическое значение, помогает студентам и школьникам лучше ориентироваться в более сложных математических дисциплинах. Современные инструменты и программное обеспечение дополнительно упрощают работу с линейными уравнениями. Использование компьютерных приложений и онлайн-калькуляторов позволяет быстро находить решения и строить графики, что способствует ускоренному обучению и повышению точности вычислений.
Однако важно понимать и владеть базовыми методами самостоятельно, чтобы иметь прочный фундамент в математике. Существуют и особенности работы с линейными уравнениями в стандартной форме, которые стоит учитывать. Например, если коэффициент B равен нулю, уравнение принимает вид Ax = C, что соответствует вертикальной прямой, и тогда невозможно выразить y через x. Аналогично, если A равен нулю, линия становится горизонтальной. Понимание таких нюансов помогает избежать ошибок при решении уравнений и их использовании в практических задачах.
Для сложных задач, когда требуется решение систем линейных уравнений, стандартная форма является удобной отправной точкой. С помощью алгебраических методов, таких как метод Крамера или метод матриц, можно эффективно находить значения переменных. Это важно в инжиниринге и науках, где часто возникает необходимость в решении системы уравнений, описывающих взаимодействующие факторы. В заключение можно сказать, что знание и умение работать с линейными уравнениями в стандартной форме — это ключевой элемент математической грамотности. Они служат базой для понимания более сложных математических структур и моделей.
Глубокое осмысление этого материала открывает широкие возможности для профессионального роста и успешного решения практических задач в различных областях деятельности.