Линейные уравнения являются одним из важнейших объектов изучения в области алгебры. Эти уравнения имеют степень один и зачастую используются для описания прямых линий на координатной плоскости. Простота их структуры и широкая применимость делают линейные уравнения основой для более сложных математических моделей, используемых в инженерии, физике, экономике и других дисциплинах. Понимание принципов, форматов и методов решения линейных уравнений значительно расширяет возможности анализа и интерпретации данных в различных сферах. Основное определение линейного уравнения связывает его с уравнениями первой степени, где переменные присутствуют в первой степени и нет произведений переменных между собой.
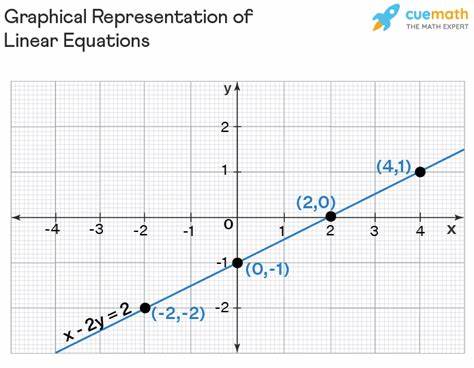
Таким образом, линейное уравнение может содержать одну, две или более переменных, при условии, что степень выражения всегда равна единице. В случае одной переменной уравнение обладает единственным решением. Например, уравнение 2x – 3 = 0 имеет единственное решение x = 3/2. Если переменных две, например, x + y = 2, то множество решений образует прямую на плоскости, представленную координатами (x, y). Количество решений увеличивается, становясь бесконечным и зависят от конкретных значений переменных, удовлетворяющих уравнению.
При трех переменных, таких как в уравнении 3x – y + z = 3, решение описывается как геометрическая поверхность в трехмерном пространстве. Важным моментом является сохранение равенства при выполнении арифметических операций над обеими сторонами уравнения. Это ключ к решению любой задачи, связанной с линейными уравнениями. Обратим внимание, что если уравнение содержит дробные коэффициенты, первый шаг заключается в освобождении переменных от дробей путём умножения обеих частей уравнения на общий знаменатель. Такой подход упрощает дальнейшие трансформации и повышает удобство вычислений.
Одной из основополагающих концепций является стандартная форма линейного уравнения. Для уравнения с одной переменной это выражение записи вида ax + b = 0, где a и b – константы, причём a не равен нулю. При наличии двух переменных уравнение представляет собой ax + by + c = 0, где x и y - переменные, а a, b, c – константы с условиями a ≠ 0 и b ≠ 0. Для трёх переменных стандартная форма имеет вид ax + by + cz + d = 0, соответствуя пространственной интерпретации. Коэффициенты a, b, c и d определяют наклон и положение прямой или плоскости.
Отдельно выделяют форму с угловым коэффициентом или наклоном — slope-intercept form. Записывается она в виде y = mx + b. Здесь m представляет собой наклон (градиент) линии, показывающий скорость изменения y при изменении x. Константа b – это точка пересечения линии с осью y. Такая форма является наиболее наглядной при графическом отображении уравнения, позволяя быстро определить ключевые характеристики прямой.
Например, уравнение y = 3x + 7 обозначает линию с наклоном 3 и смещением оси y на 7 единиц. Если рассмотреть параллельные прямые, то они имеют особое представление в slope-intercept form. Прямые, параллельные оси x, задаются уравнением y = b, где y постоянно, то есть наклон m равен нулю. Напротив, прямые, параллельные оси y, невозможно представить в виде функции y = f(x), так как наклон стремится к бесконечности. В этом случае уравнение имеет вид x = константа.
Point-slope form – ещё одна важная форма записи линейных уравнений, используемая для построения линии через заданную точку. Её формула aналогична y – y1 = m(x – x1), где (x1, y1) – координаты опорной точки, а m – наклон. Этот формат особенно удобен при определении линии по известному положению и ориентации, а также при задачах геометрии. Через элементарные алгебраические преобразования point-slope form можно привести к стандартной или slope-intercept форме, что облегчает нахождение решений и графическое изображение. Рассмотрение примеров решения линейных уравнений наглядно демонстрирует применение теории на практике.
Например, решение уравнения с одной переменной (2x – 10)/2 = 3(x – 1) ведётся через последовательные преобразования. Сначала устраняется деление, затем обе части упрощаются и переменная изолируется. Итогом становится x = –1. Системы уравнений с двумя переменными требуют использования методов, таких как подстановка, исключение и метод кросс-умножения. Например, решение системы x – y = 12 и 2x + y = 22 начинается с выражения одной переменной через другую, подставляя в второе уравнение, что позволяет находить конкретные значения переменных, например, x = 34/3, y = –2/3.
Такие системы широко используются для решения прикладных задач и имеют множество вариаций. Системы с тремя переменными становятся более сложными, требуя наличия трёх уравнений для корректного решения. Методы, как правило, основаны на матричной алгебре, поэтапном исключении переменных либо использовании вычислительной техники. Применение данного подхода встречается в инженерных расчетах и моделировании физических процессов. Глубокое понимание линейных уравнений подкрепляется знанием их форм и подходов к решению, что создаёт прочный фундамент для более продвинутых математических дисциплин.
Точное выполнение алгебраических операций, правильная организация вычислений и понимание геометрической интерпретации дают возможность эффективно работать с этим типом уравнений вне зависимости от количества переменных. Линейные уравнения также демонстрируют ключевые различия между линейными и нелинейными уравнениями. Первые всегда описывают прямые линии с постоянным наклоном, а вторые характеризуются изменяющимся наклоном и более сложной геометрией кривых. Такое различие очень важно для понимания поведения функций и анализа их графиков. Постоянное применение линейных уравнений в учебном процессе, инженерных расчетах и научных исследованиях обеспечивает их непреходящую актуальность.
Для углубленного освоения материала рекомендуется практиковаться с решениями, анализировать различные формы записи и визуализировать на графиках. Современные образовательные платформы, в том числе BYJU'S, предлагают разнообразные ресурсы, видеоуроки и тренажёры, которые делают процесс изучения более динамичным и доступным. В результате, линейные уравнения – это фундамент математики, который помогает не только решать уравнения, но и понимать и моделировать реальные миры. Освоение их основ ведет к развитию логики, аналитических навыков и умения работать с абстрактными понятиями, что высоко ценится в различных профессиональных областях.