Линейные уравнения занимают важное место в алгебре и математике в целом. Они представляют собой базовую концепцию, которая используется не только в школьной программе, но и в различных сферах науки, техники и экономики. Понимание линейных уравнений помогает решать различные задачи, связанные с моделированием процессов и анализом данных. В данной статье раскрываются основные аспекты линейных уравнений, приводятся формулы, описывается их графическое представление и приводятся примеры с подробным разбором. Линейное уравнение — это алгебраическое уравнение, у которого степень переменной равна один.
Это означает, что ни одна переменная в таком уравнении не возводится в степень выше первого, а также не является подкоренным выражением или знаменателем дроби. Благодаря этому характеристическому признаку график линейного уравнения всегда представляет собой прямую линию, что объясняет происхождение названия — «линейное». Стандартная форма линейного уравнения зависит от количества переменных. Для уравнения с одной переменной используется форма Ax + B = 0, где x — переменная, A и B — константы, причем A не равен нулю. В случае с двумя переменными стандартная форма выглядит как Ax + By = C, где x и y — переменные, A, B и C — константы.
Эта форма позволяет однозначно описывать прямую на координатной плоскости. Существует несколько способов записи линейного уравнения, которые применяются в зависимости от задачи. К ним относятся стандартная форма, форма наклона и сдвига (ссылка на пересечение с осью y), а также точечно-наклонная форма. Форма y = mx + c является одной из наиболее распространённых. Здесь m обозначает наклон (угловой коэффициент), показывающий, насколько крута прямая, а c — значение, где линия пересекает ось y.
Точечно-наклонная форма записывается как y - y1 = m(x - x1), где m — наклон, а (x1, y1) — известная точка на линии. Наклон прямой играет ключевую роль при анализе графика линейного уравнения. Он характеризует скорость изменения одной переменной относительно другой, то есть насколько y изменяется при изменении x. Если известны координаты двух точек линии, то наклон вычисляется по формуле (y2 - y1) / (x2 - x1). Положительный наклон означает, что прямая идёт вверх слева направо, отрицательный указывает на спад.
Нулевой наклон соответствует горизонтальной линии, вертикальные линии же не имеют коэффициента наклона, так как деление на ноль невозможно. Графическое представление линейных уравнений помогает визуализировать отношения между переменными и понять характер зависимости. Для уравнений с одной переменной графиком является вертикальная или горизонтальная линия, например x = a или y = b. В случае двух переменных графиком выступает прямая линия, построенная на основе множества координатных пар (x, y), удовлетворяющих уравнению. Для построения графика обычно выражают y через x, что упрощает нахождение точек и нанесение их на координатную плоскость.
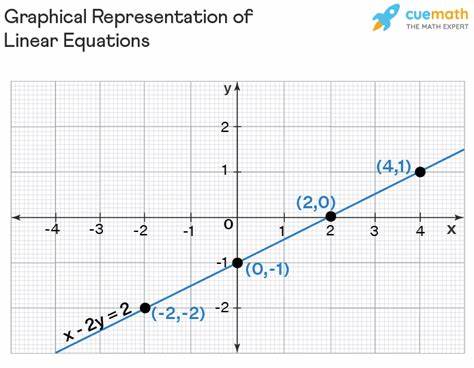
Рассмотрим пример построения графика линейного уравнения с двумя переменными. Пусть задано уравнение x - 2y = 2. Для удобства его преобразуем в форму y = mx + c: y = (x/2) - 1. Подставляя различные значения x, получают соответствующие значения y. Например, при x = 0 y равно -1, когда x = 2, y равен 0, при x = 4 y становится 1, а при x = -2 y равно -2.
Эти точки наносятся на координатную плоскость, и соединяются прямой линией, отражающей исходное уравнение. Линейные уравнения с одной переменной наиболее просты в решении. Чтобы найти неизвестную переменную, необходимо перенести все переменные в одну сторону уравнения, а числа — в другую. После этого оставшуюся часть делят или умножают, чтобы изолировать переменную. Рассмотрим уравнение 3x + 6 = 18.
Перенеся константу, получаем 3x = 12, деля обе части на 3, находим x = 4. Сложнее становятся линейные уравнения с двумя переменными, которые часто встречаются в задачах на систему уравнений. Такие уравнения можно решать разными методами: графическим, подстановки, сложения, определителей и другими. Каждый способ отличается подходом, но цель одинакова — найти значения переменных, удовлетворяющих обеим уравнениям одновременно. Не менее важным аспектом является понимание, как принципы равенства влияют на решение линейных уравнений.
Уравнение подобно весам: если на обе стороны добавить или отнять одинаковое число, равенство сохранится. Аналогично, умножение и деление обеих частей на одно и то же число (кроме нуля) не изменит решение. Это фундаментальные операции, позволяющие «перемещать» слагаемые для упрощения уравнения и поиска ответов. Важную роль в изучении линейных уравнений играют практические задачи. Например, если известно, что сумма двух чисел равна 44 и одно из чисел на 10 больше второго, можно составить уравнение x + (x + 10) = 44, где x — первое число.
Преобразовав уравнение, решаем 2x + 10 = 44, находим x = 17, следовательно, второе число 27. Такие задачи помогают лучше понять логику составления и решения уравнений. Другой пример: шесть раз большее число равно 48. Записываем уравнение 6x = 48 и находим неизвестное x = 8. Это демонстрирует, как используя линейное уравнение, можно просто и быстро найти решение реальной задачи.
Линейные уравнения могут содержать дроби, если знаменателем выступает числовое значение, а не переменная. Например, уравнение (2a/3) - 10 = 12 решается путем переноса констант и умножения обеих частей на знаменатель дроби, что позволяет избавиться от деления и упростить выражение. Такой подход расширяет возможности работы с уравнениями и повышает гибкость при решении различных задач. Различие между линейными и квадратичными уравнениями – важный аспект для понимания алгебры. В линейном уравнении переменные имеют степень один, а график всегда является прямой.
Квадратичные уравнения, напротив, содержат переменную со степенью два и формируют параболу на графике. Такая разница влияет на методы решения и интерпретацию результатов. Освоение линейных уравнений является фундаментом для более сложных математических тем. Для успешного изучения рекомендуется регулярно практиковаться в составлении и решении уравнений, анализировать графики и работать с различными формами записи уравнений. Дополнительная практика в виде задач и викторин помогает закреплять материал и развивать уверенность в своих математических навыках.
Таким образом, линейные уравнения – это мощный инструмент, который лежит в основе многих математических и прикладных дисциплин. Понимание их определения, способов записи, графического представления и методов решения открывает широкие возможности для эффективного решения разнообразных задач как в учебе, так и в реальной жизни.