Теорема вложения Такенса: ключ к пониманию хаотических динамических систем

Анализ крипторынка Новости криптобиржи

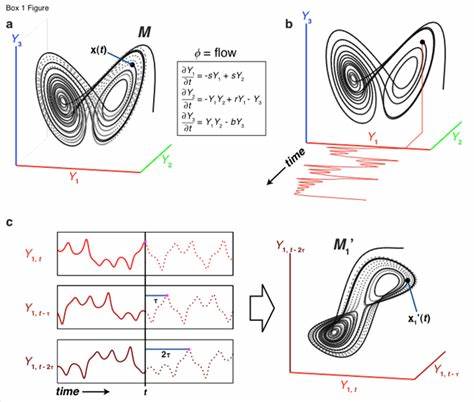
Динамические системы, особенно хаотические, долгое время оставались одной из самых сложных тем современного математического анализа и физики. Понимание поведения таких систем зачастую затруднено из-за их высокой чувствительности к начальным условиям и кажущейся случайности их траекторий. В таких условиях на помощь приходит теорема вложения Такенса — мощный инструмент, позволяющий реконструировать структуру динамической системы из наблюдаемых данных. Этот метод становится все более востребованным в различных областях науки и техники, начиная от физики турбулентности и заканчивая экономикой и биологией. Основное значение теоремы Такенса заключается в возможности восстановления «аттрактора», то есть множества состояний, к которому стремится динамическая система при своем развитии, используя лишь одну наблюдаемую величину, зависящую от состояния системы.

Аттрактор содержит всю информацию о динамике системы, и его точное восстановление позволяет изучать свойства и предсказывать поведение системы без знания полного набора исходных переменных. Таким образом, из одномерного временного ряда можно создать многомерное пространство состояний, в котором система ведет себя так же, как в изначальном техническом или физическом пространстве. Теорема формулируется следующим образом: если имеется гладкий аттрактор с определенной размерностью, то его можно интринсивно вложить в многомерное евклидово пространство при помощи так называемого «функционала наблюдения» и временных задержек этой функции. Проще говоря, из последовательных наблюдений системы с применением определенного временного лага можно построить набор координат, который окажется диффеоморфен исходному аттрактору. Это означает, что геометрические свойства и динамика системы сохраняются, несмотря на то, что изначально была доступна лишь одна измеренная величина.

Для практического применения теоремы важно правильно выбрать параметры реконструкции, в частности количество измерений пространства вложения и лаг — задержку между наблюдениями. Согласно классической формуле, минимальное число измерений должно превышать удвоенной размерности аттрактора, увеличенной на единицу. Обычно это выражается как k > 2d + 1, где d — размерность аттрактора. Слишком малая размерность приводит к наложению траекторий и потере информации, а слишком высокая увеличивает вычислительные затраты и склонна к переобучению модели. Выбор задержки также является ключевым: она не должна быть слишком мала, чтобы изменения по времени были заметны, и не слишком велика, чтобы не терять связь между параметрами.

Оптимально выбирать задержку в пределах от одной десятой до половины среднего периода орбиты на аттракторе. Эффективными инструментами для этого служат функции взаимной информации и автокорреляции, позволяющие определить временной интервал с минимальной избыточностью информации и максимальной информативностью. Применение теоремы Такенса значительно расширяет возможности анализа хаотических систем в самых разных сферах науки и техники. Прикладной интерес вызывают не только чисто теоретические вопросы, но и практические задачи, такие как прогнозирование погодных условий, изучение биологических систем, мониторинг технического состояния оборудования и экономический анализ. На практике теорема доказала свою эффективность в реконструкции известных аттракторов, например, аттрактора Рёсслера, демонстрируя корректность отображения их сложной структуры в многомерное пространство с помощью временных рядов.

Кроме того, развитие методологий на основе теоремы позволило преодолевать ограничения шума и неполных данных, что актуально для экспериментальных и естественных систем. Стоит отметить, что теорема Такенса опирается на идеи более общих результатов, таких как теорема Уитни о вложениях, и различные усовершенствования позволяют применять метод к более сложным случаям, включая нелинейные системы с фрактальной размерностью аттракторов. Важным направлением современной науки стало изучение условия «типичности» функций наблюдения и их влияния на качество реконструкции. Помимо сугубо математических аспектов, теорема вложения имеет философскую и практическую значимость. Она показывает, что из ограниченного объема информации можно извлечь существенные свойства сложных систем, а значит, прогнозировать и контролировать их поведение на основе наблюдений без полного знания законов их функционирования.

Это открывает новые горизонты в понимании природы хаоса и упорядоченности. Современные вычислительные технологии и появление мощных программных пакетов, таких как pyEDM и rEDM, облегчают применение теоремы в реальных задачах. Благодаря этому исследователи получили доступ к анализу больших и сложных наборов данных, что способствует развитию эмпирического динамического моделирования и позволяет выявлять скрытые зависимости и причинно-следственные связи в разнородных системах. Таким образом, теорема вложения Такенса является краеугольным камнем в изучении нелинейных динамических процессов. Она обеспечивает методологическую основу для реконструкции и анализа хаоса, раскрывая структуру и закономерности, лежащие в основе кажущейся случайности.

В будущем ожидается дальнейшее развитие теоретической базы и совершенствование экспериментальных подходов, что позволит расширить применение метода в новых областях — от медицины до экологии и робототехники. В условиях роста объемов данных и сложности исследуемых систем, значимость возможности надежной реконструкции динамики на основе ограниченного числа наблюдений будет только возрастать. Это делает теорему Такенса одним из важнейших инструментов современной науки и техники.