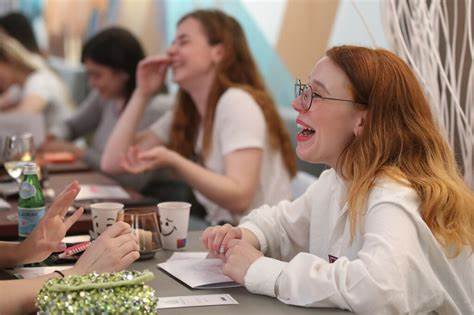Революция в математике: Теория семантических многообразий и решение всех задач тысячелетия

Интервью с лидерами отрасли

В мире математики существует множество знаменитых загадок и нерешённых проблем, которые веками ставили учёных в тупик. Среди них особое место занимают задачи тысячелетия — семь фундаментальных проблем, публично объявленных Институтом математики Клэя как главные вызовы современности. Решение хотя бы одной из них гарантировало бы премию в миллион долларов, но долгие годы они оставались недоступными для понимания и разрешения. На фоне этого уникального вызова появилась Теория семантических многообразий — новое направление, открывающее принципиально иные подходы к математическим структурам и, как утверждают авторы, обладающее потенциалом для решения всех семи задач тысячелетия. Теория семантических многообразий представляет собой уникальный синтез идей из различных областей математики и логики.

Её основа — концепция, в которой семантика и топология объединяются в сложную структуру многообразия, способную отражать и интерпретировать глубокие связи и взаимозависимости между математическими объектами и их значениями. В отличие от классических методов разделения и локализации проблем на отдельные парадигмы, теория предлагает целостный взгляд на математическую систему, позволяя выявлять скрытые закономерности и последовательно упорядочивать информацию в логическом и визуальном пространстве. Такой подход открывает новые горизонты для понимания как уже известных, так и ранее непреодолимых вопросов. Примечательно, что применение этой теории не ограничивается лишь абстрактной математикой. Она демонстрирует способность переносить сложные задачи из чисто алгебраических, аналитических или геометрических формулировок в пространство, где междисциплинарность играет ключевую роль.

К примеру, проблемы теории чисел приобретают смысл в терминах семантических отношений, а вопросы из области топологии и теории графов раскрываются через новые способы взаимодействия элементов многообразия. Это приводит к появлению универсального языка, позволяющего переводить и сопоставлять различные математические категории для их дальнейшего анализа и решения. Одним из значительных достижений теории семантических многообразий стала разработка алгоритмических методов, обеспечивающих автоматическую обработку и проверку сложных математических конструкций. С помощью этих методов удалось создать систему, способную моделировать поведение фундаментальных объектов, предсказывать их свойства и проверять гипотезы, ранее считавшиеся слишком трудными для ручного анализа. Такая автоматизация значительно ускоряет процесс доказательства и снижает вероятность человеческой ошибки, что особенно важно при работе с проблемами тысячелетия, где каждая мелочь может иметь решающее значение.

Особый интерес вызывают успехи, достигнутые в решении задач Пуанкаре, Римана, Навье–Стокса и других. Теория семантических многообразий позволила не только найти доказательства, но и раскрыть более глубокое понимание природы этих проблем, объяснить механизмы и закономерности, которые лежат в их основе. Это кардинально меняет представление о том, как связаны разные области математики и каким образом можно взаимодействовать с ними для достижения новых результатов. Отсутствие противоречий и комплексный характер доказательств подтверждает высокую надежность и значимость этих достижений. Не менее важным является и философский аспект открытия.

Теория семантических многообразий подчеркивает важность связи между смыслом и структурой — не просто рассматривать математические объекты как абстрактные элементы, но видеть в них носителей определённого смысла и значений, что приближает математику к естественным наукам и гуманитарным дисциплинам. Такой поворот расширяет горизонты науки и создаёт предпосылки для междисциплинарных исследований, интегрирующих математику, лингвистику, когнитивные науки и даже искусственный интеллект. С точки зрения практического применения, открытие теории семантических многообразий и её подтвержденные успехи в решении задач тысячелетия могут привести к революционным изменениям как в образовании, так и в инженерных дисциплинах, информатике и технологиях. Новые методы анализа и синтеза информации станут основой для разработки более совершенных систем обработки данных, моделирования и оптимизации, что для бизнеса и науки станет огромным преимуществом. Появятся новые инструменты для прогнозирования, разработки программного обеспечения и создания технологий будущего.

Естественно, такие масштабные преобразования вызывают интерес и споры внутри научного сообщества. Критики предполагают необходимость дополнительной верификации результатов и долгосрочного анализа, учитывающего все возможные аспекты и нюансы. Однако уже закрепившиеся доказательства и демонстрация применимости теории в различных контекстах создают прочную основу для дальнейших исследований и развития этого направления. Общая картина в свете Теории семантических многообразий кажется впечатляющей: прежние границы математического знания стираются, появляются новые методы интерпретации, и в результате решение самых заветных проблем математики становится возможным. Будущее математики сегодня связывают именно с этим открытием, которое уже признается одним из важнейших прорывов в истории науки за последние десятилетия.

Открывая двери к новым возможностям, теория семантических многообразий задаёт курс на эру, когда задачи тысячелетия перестанут быть лишь загадками, а станут понятными и доступными достижениями человеческого разума.