Логистическая регрессия — это мощный и широко применяемый метод в статистике и машинном обучении, который помогает предсказывать вероятность наступления события с бинарным исходом. В современном мире аналитики и дата-сайентисты часто сталкиваются с задачей классификации, когда исходом должно быть одно из двух возможных состояний — например, да или нет, успех или неудача, болезнь или здоровье. Логистическая регрессия идеально подходит для таких сценариев, и она играет ключевую роль в различных сферах, от медицины до финансовых технологий. Главная цель логистической регрессии — прогнозирование вероятностей принадлежности объекта к одному из двух классов на основе набора независимых переменных или признаков. Эти признаки могут включать в себя возраст пациента, пол, вес, образ жизни, поведение клиента и многое другое.
Важным отличием логистической регрессии от линейной является то, что результат модели — вероятность - ограничена интервалом от нуля до единицы, что соответствует смыслу вероятности. Чтобы понять, как работает логистическая регрессия, необходимо познакомиться с понятием «шансов» и «отношения шансов». Шанс (odds) — это отношение вероятности наступления события к вероятности его ненаступления. Например, если вероятность равна 0.7 (70%), то шанс будет 0.
7 делённый на 0.3, что равно приблизительно 2.33. Отношение шансов сравнивает шансы между двумя группами и показывает, во сколько раз событие более вероятно в одной группе по сравнению с другой. Это фундаментальная метрика в медицине, маркетинге и других областях.
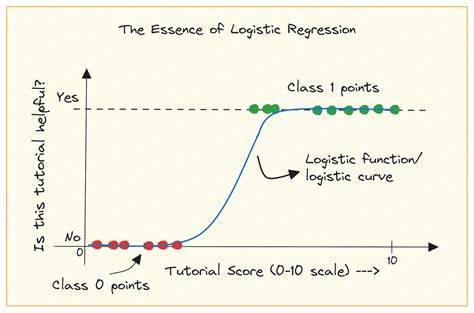
Основой математической модели логистической регрессии является использование сигмоидальной функции, которая преобразует линейную комбинацию признаков модели в выходное значение от 0 до 1. Сигмоидальная функция берет входное значение и с помощью экспоненты превращает его в вероятность. График этой функции имеет форму буквы S: для очень больших или очень малых значений входного сигнала выход стремится к 1 или 0 соответственно, при этом вблизи нуля вероятность изменяется наиболее резко. Логистическая регрессия моделирует логарифм отношения шансов как линейную комбинацию признаков, то есть мы прогнозируем логарифмические шансы, исходя из данных. Таким образом, расчет вероятности происходит через обратное преобразование логарифма — именно это и делает сигмоидальная функция.
При обучении модели используется метод максимального правдоподобия (maximum likelihood estimation, MLE), который ориентирован на поиск таких коэффициентов модели, при которых вероятность наблюдаемых данных максимальна. В отличие от обычной линейной регрессии, где применяется минимизация функции ошибки (например, среднеквадратичная ошибка), в логистической регрессии происходит итеративный процесс оптимизации, часто с использованием градиентного подъема или специализированных алгоритмов, таких как 'liblinear' или 'lbfgs'. Важной частью анализа является деление данных на обучающую и тестовую выборки. Это необходимо для оценки качества модели на новых данных и предотвращения переобучения. Перед подачей данных на вход модели признаки часто масштабируют, чтобы они находились в сопоставимых диапазонах.
Это может значительно улучшить работу оптимизационного алгоритма и повысить итоговую точность предсказания. После того как модель обучена, можно сделать прогнозы для новых случаев с помощью метода predict, который обычно использует порог 0.5 — если прогнозируемая вероятность события превышает 50%, объект относится к первому классу, иначе к второму. При необходимости этот порог можно изменить для баланса между точностью и полнотой классификации. Метод predict_proba позволяет получить не просто класс, а саму вероятность принадлежности к каждому из классов, что позволяет более гибко подходить к принятию решений.
Одной из проблем, связанных с использованием сигмоидальной функции, является эффект затухающего градиента. Когда значения функции стремятся к 0 или 1, производная становится очень маленькой, что усложняет обучение сложных моделей, например, глубоких нейронных сетей. По этой причине в современных подходах к глубокому обучению часто применяют альтернативные функции активации. Логистическая регрессия не ограничивается только бинарной классификацией. На практике её расширяют для мультиклассовых задач, где объект классифицируется в одну из трёх и более категорий.
Это достигается с помощью методов вроде «мультино́мальной» логистической регрессии или создания набора бинарных моделей по схеме «один против всех». При этом кодирование и методы обучения остаются схожими, что позволяет использовать имеющиеся инструменты и библиотеки без существенных изменений. В программировании для решения задач логистической регрессии популярна библиотека scikit-learn на Python. Она предоставляет простой и понятный интерфейс для подготовки данных, обучения модели, её оценки и предсказания. Важные этапы включают масштабирование признаков с помощью StandardScaler, разбиение данных на обучающую и тестовую выборки через train_test_split, обучение модели с помощью LogisticRegression и последующую оценку точности с accuracy_score и classification_report.
Применение логистической регрессии охватывает множество сфер. В медицине она используется для прогнозирования вероятности заболевания или выживания пациентов в зависимости от их истории болезни и текущего состояния. В финансовой области данный метод помогает выявлять мошеннические транзакции или кредитоспособность клиентов. В маркетинге логистическая регрессия позволяет предсказывать вероятность отклика на рекламные компании или вероятность оттока клиентов. Благодаря очевидной интерпретируемости коэффициентов модели она остаётся популярной для ситуаций, где важно не только получить прогноз, но и понять влияния конкретных факторов.
Стоит отметить, что несмотря на кажущуюся простоту и очевидность, логистическая регрессия имеет нюансы, которые необходимо учитывать. Например, тесная корреляция между признаками (мультиколлинеарность) может искажать оценки коэффициентов, что снижает качество модели. Баланс классов важен — при сильном перекосе данных в сторону одного класса модель может быть склонна предсказывать чаще именно его, что снизит качество распознавания редких случаев. Помимо качественной подготовки данных и правильной настройки параметров модели, существует множество расширений и модификаций логистической регрессии, таких как регуляризация (L1, L2) для борьбы с переобучением, использование различных функций потерь, а также интеграция в ансамблевые методы. В итоге, логистическая регрессия — один из столпов машинного обучения и статистического анализа, сочетание простоты, мощности и понятности которого делает её привлекательной для решения множества задач классификации.
Освоение принципов работы, математических основ и практических приёмов использования логистической регрессии — важный шаг для каждого, кто занимается обработкой данных и моделированием. Грамотное применение этого метода позволяет не только строить точные предсказания, но и глубже понимать зависимости внутри данных, формируя основу для более сложных и эффективных моделей.