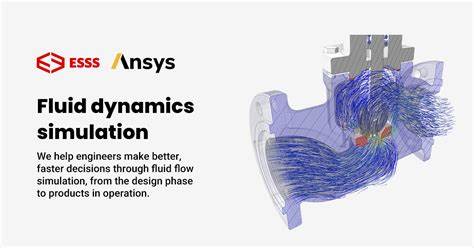
Представьте себе простую чашку воды. Казалось бы, это обыденный объект, не содержащий сложных вычислительных механизмов. Однако недавнее открытие в области математики и физики показало нечто феноменальное: потоки жидкости способны функционировать как полноценные вычислительные устройства, способные выполнять любые алгоритмы. В середине 2025 года ученые доказали, что уравнения Навье – Стокса, описывающие движение жидкости, обладают свойствами так называемой вычислительной полноты по Тьюрингу. Иными словами, определенные виды жидкости могут имитировать работу любого компьютера.
Этот научный прорыв ставит новое ограничение перед искусственным интеллектом и его возможностями предсказывать поведение некоторых физических систем. Если жидкость способна выступать в роли универсальной вычислительной системы, то предсказать исход ее течения оказывается настолько же сложно, как решить запретную в теории вычислимости задачу останова – классическую задачу, доказано, что для нее нет универсального алгоритма решения. Таким образом, даже самый мощный ИИ и суперкомпьютеры не смогут преодолеть эту фундаментальную преграду. Основой для понимания этого феномена служат уравнения Навье – Стокса, созданные в XIX веке и до сих пор остающиеся одним из самых важных, но сложных описаний движения жидкостей и газов. Эти дифференциальные уравнения описывают изменение скорости и давления жидкости во времени и пространстве, учитывая вязкость и другие физические параметры.
Математики и физики на протяжении веков боролись с исследованием их решений, пытаясь предсказать, будут ли решения «хорошо себя вести» или возникнут сингулярности и катастрофические изменения за конечное время. Несмотря на столетия интенсивных исследований, самые сложные вопросы в этой области остаются открытыми и даже награждены премиями в миллион долларов. Понятие вычислительной полноты по Тьюрингу происходит из теории алгоритмов и компьютерной науки. Система называется тьюринг-полной, если она способна выполнять любые вычисления, которые выполнил бы универсальный компьютер или алгоритм. Эта идея была впервые предложена Аланом Тьюрингом в середине XX века и стала краеугольным камнем теоретической информатики.
Если физическая система, например жидкость, может моделировать любые алгоритмы, значит, ее поведение не поддается общему предсказанию, поскольку задачи останова для таких систем являются неразрешимыми в общем случае. Связь с задачей останова уходит корнями в работы самого Тьюринга, который в 1936 году доказал невозможность создания алгоритма, способного с уверенностью определить, когда любая программа остановится. Аналогично, если поток жидкости запрограммировать на выполнение вычислений, связанные с проверкой «остановится ли процесс», то предельная судьба частицы в таком потоке оказывается неразрешимой проблемой. Это означает, что нет универсального решения, которое смогло бы ответить на все подобные вопросы о поведении жидкости, вне зависимости от времени и ресурсов вычисления. Идея о том, что жидкостный поток может выступать в роли вычислительной машины, витала в научном сообществе десятилетиями.
Еще в 1991 году математик Кристофер Мур выдвинул гипотезу о том, что динамические системы, включая гидродинамику, способны на сложные вычисления, превышающие обычное понятие хаоса. Его работы заложили основу для обсуждения «непрогнозируемости сверх хаоса» в физике. Позже, в 2010-х, Fields медалист Терренс Тао предложил гипотезу о том, что уравнения идеальной жидкости (уравнения Эйлера) могут обладать вычислительной полнотой. Он даже предположил, что запрограммировав жидкость на выполнение бесконечной вычислительной задачи, можно вызвать так называемый «выброс» решения, когда течение становится бесконечно неспокойным. Утверждение, что идеальные жидкости могут быть вычислительно универсальными, было подтверждено в 2021 году группой ученых, опубликовавших работу, где доказали тьюринг-полноту стационарного течения идеальной жидкости, заданного на особом трехмерном пространстве.
Однако в реальном мире жидкости обладают вязкостью, и их описывают более сложные уравнения Навье – Стокса. Вопрос о том, может ли вязкость препятствовать вычислительной универсальности, оставался открытым – поскольку она является фактором трения и затухания, который обычно сглаживает и подавляет сложные динамические структуры. Летом 2025 года эта загадка была решена. Группа исследователей во главе с Сёреном Диром и его коллегами создала математическую конструкцию стационарных решений уравнений Навье – Стокса с вязкостью, которые обладают вычислительной полнотой по Тьюрингу. Используя продвинутые методы дифференциальной геометрии и топологии, ученые обнаружили, что под определенными условиями три измерения могут принимать структуру, позволяющую сохранять сложные вычислительные потоки, несмотря на вязкостные потери.
Это означает, что даже реальные жидкости способны в принципе выполнять любые вычисления, а их поведение в определенных конфигурациях не поддается алгоритмическому предсказанию. На практике это подтверждает наличие фундаментальных пределов в моделировании и прогнозировании сложных физических процессов. Любая попытка ИИ создать абсолютно точную и универсальную модель поведения таких систем обречена из-за заложенных в них логических ограничений, а не только из-за технических или вычислительных трудностей. Чтобы лучше понять, как именно можно «запрограммировать» жидкость, исследователи применили геометрические методы, сводящие вычислительные процессы к топологии потоков. Идея в том, что траектории частиц жидкости (их стримлайны) соответствуют вроде бы простым геометрическим объектам, способным кодировать состояние и шаги работы вычислительной машины.
Если машина «останавливается», частица достигает целевой области; если нет, то ее путь бесконечно продолжается. Таким образом, наблюдение за движением разрешает косвенно оценить вычислимость задачи. С точки зрения искусственного интеллекта, подобное открытие имеет широкие последствия. Сегодня ИИ активно используется для прогнозирования погоды, моделирования климата, проектирования самолетов и многого другого, где управлять потоками жидкости и газа критично. Все эти задачи основываются на предположении, что с достаточной вычислительной мощностью и точными алгоритмами можно получить точные прогнозы.
Но открытие вычислительной полноты в уравнениях Навье – Стокса ставит под сомнение эту веру в универсальность предсказания. Оно напоминает о том, что даже гипотетический «демон Лапласа» с полной информацией о системе может столкнуться с принципиальной непредсказуемостью. Разумеется, не все реальные сложные течения жидкости оказываются тьюринг-полными в практическом смысле – для этого нужны специальные конфигурации, которые нельзя найти в обыденных обстоятельствах. Однако сам факт существования подобной теоретической возможности заставляет пересмотреть фундаментальные рамки науки и искусственного интеллекта. Для исследователей это сигнал к тому, что необходимо учитывать ограничения не только вычислительных ресурсов, но и самой природы задачи.
Такое понимание открывает двери к новой междисциплинарной работе, где математики, физики, специалисты по ИИ и теории вычислимости объединяют свои знания, чтобы распознать моменты, когда модель попадает в «зону неразрешимости». Будущие модели и алгоритмы могут быть адаптивными, учитывающими существование«труднопредсказуемых» режимов и применяющими альтернативные стратегии или предоставляющими вероятностные оценки вместо точных прогнозов. Философский аспект также важен. Открытие ставит под сомнение давнюю мечту о всесильном искусственном интеллекте, способном предсказывать каждый аспект мира с абсолютной точностью. На самом деле идеальные предсказания невозможны не из-за хаотичности или шумов, а из-за ограничений, встроенных в саму логику и математику, управляющую Вселенной.
Это создает гораздо более реалистичный взгляд на потенциал ИИ, где успехи приходят с признанием границ возможностей. В дополнение к научному значению, результаты исследователей могут иметь влияние на образование и технологические сообщества. Понимание того, что в вычислительной физике существуют фундаментальные ограничения, поможет лучше готовить специалистов в области ИИ, физики и математики, обучая их не только методам моделирования, но и теоретическим основам вычислимости. Кроме того, знание потенциала технологий и программного обеспечения, предлагаемых для студентов в области ИИ, может ускорить прогресс и распространять передовые знания шире. В заключение, в мире, где границы между физикой, математикой и компьютерной наукой стираются, открытие вычислительной полноты в уравнениях Навье – Стокса показывает глубину и сложность мира жидкостей и движущихся сред.
Можно сказать, что сама природа способна к вычислениям, и эти вычисления определяют поведение систем, которые нам казались просто хаотичными. Теперь предстоит новая эпоха, когда исследователи будут учитывать эту фундаментальную сложноразрешимость при построении моделей и прогнозов, особенно в области искусственного интеллекта и науки о данных. Мир становится одновременно удивительнее и сложнее, чем мы могли себе представить, и именно знание об этих границах позволяет двигаться вперед с осознанием, что не все поддается устойчивому предсказанию, несмотря на технологический прогресс.