Решение шестой задачи Гильберта: Вывод уравнений гидродинамики через кинетическую теорию Больцмана

Новости криптобиржи

Шестая задача фонда Дэвида Гильберта, сформулированная в начале XX века, относится к фундаментальным проблемам математической физики. Задача ставит целью разработку строгого математического перехода от атомистической модели материи, описываемой законами Ньютона, к уравнениям гидродинамики, которые определяют поведение жидкостей и газов в масштабах, гораздо больших, чем размеры отдельных молекул. Этот переход является краеугольным камнем в понимании физических процессов на разных масштабах и служит основой для современной теории газовой динамики и гидродинамики. Одним из основных инструментов решения этой задачи выступает кинетическая теория Больцмана, предложенная Людвигом Больцманом в XIX веке. Она описывает эволюцию функции распределения молекул в пространстве и импульсе, позволяя связать микроскопические взаимодействия частиц с макроскопическими потоками вещества и энергии.

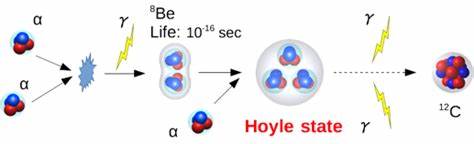
В последние годы значительный прогресс в решении шестой задачи Гильберта был достигнут благодаря работам, которые предложили строгий и полный вывод фундаментальных уравнений гидродинамики, таких как сжимаемые уравнения Эйлера и несжимаемые уравнения Навье-Стокса-Фурье, непосредственно из кинетической теории. Одной из наиболее заметных и важных работ в этом направлении является работа группы математиков, которая продемонстрировала данный переход, начиная с микроскопической модели твёрдых сфер, описывающих частицы, сталкивающиеся упруго. Эти исследователи использовали жесткий математический аппарат, расширяя и совершенствуя результаты предыдущих исследований, и в частности подтверждают применение уравнения Больцмана на торусе в двух и трёх измерениях. Традиционно уравнение Больцмана рассматривается в бесконечном пространстве, однако работа с компактными ориентированными многообразиями, такими как тор, существенно усложняет анализ, требуя нового подхода к получению оценок и транспортных свойств. Именно эти нововведения сделали возможным строгое доказательство перехода от кинетического описания к уравнениям гидродинамики.

Важным аспектом достижений является развитие метода, позволяющего на основе систем частиц с заданными законами движения — в частности системы упруго сталкивающихся твёрдых сфер — строить предельный процесс, который в конечном итоге приводит к описанию, которое традиционно используется в гидродинамике. Это означает, что фундаментальные уравнения, которыми до сих пор пользуются инженеры и физики для моделирования течений жидкостей и газов, имеют строгую математическую основу, исходящую из законов классической механики. Кроме того, данное достижение укрепляет взаимосвязь между различными уровнями описания природы, объединяя микроскопическую и макроскопическую физику. До этого момента существовали лишь приближённые методы, часто использовавшиеся в физике и инженерии для вывода уравнений гидродинамики, однако они были лишены строгой математической валидации. Новое доказательство служит решением важнейшей открытой проблемы, поставленной Гильбертом, и открывает путь для дальнейшего расширения модели, включая более сложные взаимодействия и процессы.

Следует отметить, что эти достижения имеют не только теоретическое значение, но и практическое влияние на многие отрасли. Моделирование течений газов и жидкостей лежит в основе аэродинамики, метеорологии, производства и других научно-технических областей. Полная математическая строгость в выводе уравнений повышает надежность и точность численных моделей, что в свою очередь способствует развитию технологий. Также важной темой в контексте шестой задачи Гильберта является роль нелинейности и возмущений. Уравнения гидродинамики, такие как уравнения Навье-Стокса, сами по себе являются нелинейными и порождают сложные явления, включая турбулентность.

Понимание того, как эти нелинейные эффекты возникают из молекулярного уровня, увеличивает глубину нашего физического понимания и способствует новым открытиям в области динамики жидкостей и газов. Впереди остается ряд открытых вопросов и направлений, в которых развитие теории будет способствовать как фундаментальным исследованиям, так и практическим приложениям. Например, музыка многофазных и реактивных сред, расширение кинетической теории для включения квантовых эффектов, а также анализ различных форм столкновений и взаимодействий между частицами. Учёные по всему миру продолжают работать в этом направлении, чтобы предложить еще более общие модели и методы, способные описать широкий спектр физических систем. В результате последних исследований вопросов, связанных с шестой задачей Гильберта, можно с уверенностью утверждать, что пришло эпохальное понимание перехода от микромира к макромиру в контексте гидродинамики.

Это хороший пример эффективного соединения математики, физики и инженерии, что делает эту тему особенно привлекательной как для ученых, так и для практиков. В свете изложенного становится очевидным, что решение шестой задачи Гильберта — это не просто историческая веха, а живой и развивающийся процесс, который продолжит влиять на развитие науки и техники в будущем. Это достижение открывает новые горизонты для изучения сложных физических систем и их математических моделей, делая наш мир более понятным и управляемым с научной точки зрения.