В современном мире математики и компьютерных наук задачи, связанные с визуализацией и моделированием сложных геометрических объектов, становятся все более актуальными. Одним из таких направлений является поиск встраиваний регулярных карт и полиэдров. Здесь на сцену выходит Beryl — мощный решатель полиэдров, разработанный специально для эффективного нахождения встраиваний регулярных карт, а также оптимизации полиэдров на основе списка треугольников с минимизацией пересечений. Это уникальное программное обеспечение, обладающее как научной, так и практической ценностью, заслуживает особого внимания в сообществе геометрических исследований и 3D-моделирования. Beryl представляет собой проект с открытым исходным кодом, написанный на C++ и использующий библиотеку Eigen для реализации алгоритмов линейной алгебры.
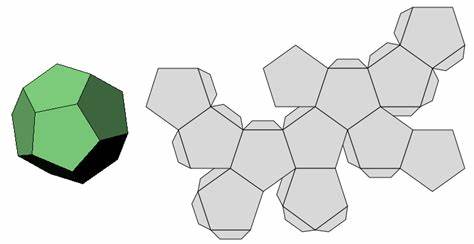
Библиотека Eigen — это заголовочная библиотека, что упрощает процесс установки и использования, поскольку не требует дополнительной сборки. Проект легко компилируется на популярных платформах, включая Windows, Mac OS и Linux, что делает его универсальным инструментом для широкого круга пользователей и разработчиков. Основное предназначение Beryl — поиск встраиваний регулярных карт. Регулярные карты — это обобщение понятий многоугольников и полиэдров на поверхности с разной топологией, например, на поверхности тора или более сложных поверхностях. Каждый такой объект можно представить в виде разбиения поверхности на области с определёнными симметриями и структурой.
Важной задачей является найти способ отобразить такую структуру в трёхмерном пространстве без пересечений рёбер, что соответствует корректному встраиванию полиэдра или карты. Для реализации этой задачи Beryl использует список треугольников, представляющих собой разбиение поверхности, и, опционально, список автоморфизмов — симметрий карты, которые ускоряют процесс поиска решения. Поддержка симметрий является важной особенностью, так как позволяет значительно сократить время вычислений за счет ограничения пространства поиска на симметричные варианты расположения вершин. Благодаря этому подходу многие регулярные карты с родом менее 100 могут быть найдены и визуализированы с помощью Beryl с минимальными усилиями. Процесс решения задачи делится на два ключевых этапа.
Первый — основной решатель, который путем алгоритмических проверок и итеративного поиска пытается найти геометрическое расположение вершин, минимизирующее пересечения рёбер. Если же полностью избежать пересечений не удаётся или требуется улучшение качества решения, на помощь приходит второй этап — уточняющий решатель, или рефинемент-солвер. Он служит для улучшения эстетики и качества ранее найденного решения за счёт повышения расстояний между вершинами, сглаживания острых углов и создания более структурированной и визуально приятной модели. Особенностью Beryl является возможность работы с разнообразными вариантами симметрий, что базируется на заранее подготовленных данных о возможных автоматизмах и геометрических симметриях регулярных карт. Пользователь может выбрать конкретную симметрию, подставить её в командную строку программы и запустить поиск решения для этой конфигурации.
Для каждого варианта симметрии можно получить не только результат с минимальными пересечениями, но и изучить характерные особенности и варианты перестановок, что помогает в проведении глубокого анализа структуры карты. Важно отметить, что Beryl поддерживает поиск двойственных встраиваний, что расширяет возможности моделирования и понимает взаимосвязи между различными типами карт и полиэдров. Двойственные карты действительно широко используются в теории графов и геометрии, и их корректное нахождение обеспечивает более полное знание о классах полиэдров и их свойствах. Отдельного упоминания заслуживает поддержка расширенных функций, таких как настройка координат вершин на целочисленной сетке с определённым масштабом. Это особенно полезно при работе с алгоритмами, для которых важна точная геометрия и соответствие сетке, например, при интеграции в другие программные среды или разработке приложений, связанных с компьютерной графикой и цифровым дизайном.
Однако при использовании такой функции необходимо учитывать ограничения по симметрии, так как не все типы симметрий могут быть реализованы при условии фиксации координат на сетке. Помимо основной функциональности, Beryl предлагает удобные инструменты для экспорта результатов. Это может быть экспорт проводной модели (wireframe) или специальных срезов полиэдра, что облегчает визуализацию и дальнейшую работу с найденными встраиваниями в других системах. Поддержка сообщества и постоянное развитие делают Beryl особенно привлекательным для научного и инженерного сообщества. Публикации, видеообзоры и интерактивные визуализаторы позволяют быстрее освоить инструмент и расширить свою базу знаний в области симметрий и топологии полиэдров.
Программа также легко интегрируется с современными средствами разработки, что упрощает создание новых исследовательских проектов и практических приложений. Подытоживая, Beryl — это мощный, гибкий и эффективный решатель для встраивания регулярных карт и оптимизации полиэдров. Он сочетает в себе теоретическую глубину и прикладную полезность, позволяя решать сложные задачи топологического и геометрического характера с высокой степенью надежности и в разумные сроки. Его функциональность и расширяемость делают его ценным инструментом для ученых, инженеров и разработчиков, работающих с многогранниками, симметриями и сетевыми структурами в трехмерном пространстве. Использование Beryl открывает новые горизонты в исследовательской деятельности, позволяя визуализировать и моделировать сложные объекты с удивительной точностью и гибкостью.
В сочетании с современными вычислительными мощностями это программное обеспечение способно существенно упростить многие задачи в области математики, компьютерной графики и дизайна, а также вдохновить на создание новых форм и структур в науке и искусстве.