В современном мире науки о данных и машинного обучения ключевым аспектом успешной работы алгоритмов является надежность и стабильность численных вычислений. Важность этой темы нельзя переоценить, особенно когда речь идет о преобразовании числовых данных в вероятности или ранжировании объектов на основе определенных метрик. Среди множества функций активации и нормализации в нейронных сетях и статистических моделях SoftMax занимает особое место. Тем не менее, несмотря на свою популярность и широкое использование, классическая функция SoftMax обладает серьезным недостатком — она подвержена числовой нестабильности, которая может существенно исказить результаты анализа и классификации. Здесь на помощь приходит LogSoftMax, альтернативный подход, который значительно улучшает устойчивость вычислений и позволяет получать более корректные результаты.
SoftMax несет в себе истоки из статистической физики, а именно из концепции Болцмановского фактора. Он преобразует набор числовых значений в вероятности, суммирующиеся к единице, используя экспоненту каждого значения, нормализованную по сумме всех экспонент. Это позволяет «распределять» вероятности между классами, что чрезвычайно важно в задачах классификации, где итоговая вероятность принадлежности к каждому из классов служит базой для принятия решений. Однако использование экспоненты — функции, часто быстро возрастющей, может привести к тому, что если одно значение намного больше остальных, оно становится доминирующим, и вероятности других классов стремятся к нулю. Это явление формирует так называемую числовую нестабильность, приводящую к потере информации и искажению результатов.
Чтобы проиллюстрировать данную проблему, рассмотрим пример с оценками команд. Пусть у нас есть четыре команды с оценками, например 1.4, 1.5, 1.6 и 170.
При применении классического SoftMax получается, что вероятность для команды с рейтингом 170 равна практически единице, а для остальных — ровно нулю. Такое распределение не отражает действительных различий между командами с маленькими значениями, просто нивелируя их в пользу явно лидирующей. В реальных задачах это может нарушить процесс ранжирования, классификации или обучения модели и привести к неправильным выводам. LogSoftMax решает эту проблему, преобразуя вычисления в логарифмическую область. Вместо прямого применения экспоненты и последующего суммирования, LogSoftMax вычисляет логарифм от экспоненты с вычитанием логарифма суммы всех экспонент.
Такая манипуляция с числами значительно снижает вероятность возникновения переполнения или потери точности при работе с большими величинами. В нашем примере команды получат значения, позволяющие сохранить относительный порядок и различия между ними, что сделает классификацию и ранжирование более информативными и полезными. С точки зрения числовой математики, работа с логарифмами — стандартная практика для стабилизации вычислений, особенно когда в расчетах часто присутствуют экспоненциальные функции. Эта методика широко применяется в статистике, например, при вычислении вероятностей в гауссовых распределениях, максимальном правдоподобии и других задачах. В контексте глубинного обучения LogSoftMax не только предотвращает взрыв чисел, но и позволяет упростить вычисление градиентов, что способствует более эффективному обучению нейронных сетей.
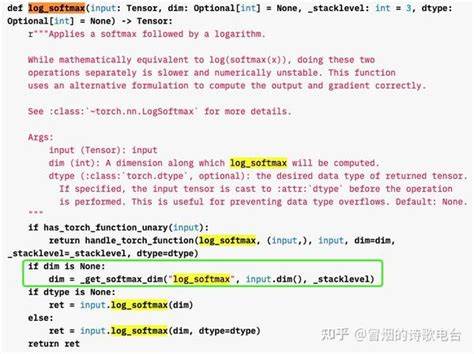
Применение LogSoftMax особенно актуально в задачах с большими диапазонами значений или при работе с глубокими архитектурами, где переполнение чисел может привести к сбоям модели, плохой сходимости или даже полной остановке обучения. Логарифмическое преобразование нормализует значения и устраняет чрезмерные перепады между оценками, что позволяет добиться более равномерного и корректного распределения вероятностей. Для практиков в области машинного обучения и науки о данных данный факт стоит воспринимать как важный технический совет: использование LogSoftMax вместо классического SoftMax не только повышает числовую надежность, но и способствует более точным предсказаниям и стабильной работе модели. В известных библиотеках, таких как PyTorch, предусмотрена встроенная функция log_softmax, которая облегчает интеграцию этой техники в рабочие процессы без дополнительных сложностей. Желание разработчиков и исследователей создавать устойчивые и качественные алгоритмы обуславливает рост популярности LogSoftMax.
На фоне растущих сложностей моделей и все более требовательных приложений, связанных с большими объемами данных и огромными вычислительными нагрузками, устойчивость алгоритмов становится одной из главных задач. Стоит отметить и то, что концепция логарифмического преобразования функций не ограничивается только SoftMax. Во многих статистических и вероятностных методах работа с логарифмами является обязательной частью процедур из-за своей способности предотвращать числовые ошибки и помогать в интерпретации результатов. Таким образом, выбор между классическим SoftMax и LogSoftMax идет не только по критерию удобства, но и с позиции точности и стабильности вычислений. Если говорить об общих рекомендациях, то для большинства сложных и требовательных задач рекомендуется отдавать предпочтение LogSoftMax как более устойчивому и надежному инструменту.
Итогом становится понимание того, что в мире науки о данных качественные и стабильные вычисления — это неотъемлемая часть успеха. Правильный выбор функций активации и нормализации, таких как LogSoftMax, помогает избежать распространенных ошибок и повысить эффективность алгоритмов. Это особенно важно для методов машинного обучения, где точность и надежность результата имеют первостепенное значение. Инструмент LogSoftMax — это не просто альтернатива, а практическое решение, повышающее качество моделей, сохраняющее информацию и обеспечивающее устойчивость вычислений. Его использование уже сегодня становится стандартом в разработке и исследовании современных алгоритмов обработки данных и искусственного интеллекта.
Любой специалист, стремящийся создавать надежные и точные модели, должен учитывать преимущества LogSoftMax, осознавая, что даже малейшие числовые неточности могут привести к неправильным выводам и сделкам срешением. Именно поэтому LogSoftMax заслуженно занимает важное место среди методов стабильной нормализации в машинном обучении и статистике, делая вычисления прозрачными, надежными и информативными.