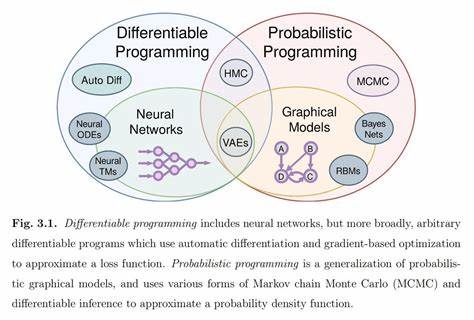
Современный мир стремительно меняется цифровыми технологиями и методами анализа данных. Среди множества инструментов и техник особое место занимает дифференцируемое программирование — относительно новая, но быстро набирающая популярность концепция. Для многих людей, даже тех, кто боится сложной математики, она открывает двери к эффективному решению задач оптимизации без необходимости разбираться в сложных уравнениях и вычислениях. Но что именно представляет собой дифференцируемое программирование? Почему оно становится столь востребованным в науке о данных, машинном обучении и искусственном интеллекте? И как при помощи современных библиотек можно быстро и просто реализовать оптимизацию в собственных проектах? Эти и другие вопросы мы рассмотрим в нашем подробном разговоре. Дифференцируемое программирование — что это? Дифференцируемое программирование — это подход к программированию, при котором функции и вычисления записываются так, чтобы можно было автоматически вычислять их производные или градиенты.
Традиционно это связано с методами математики, такими как дифференцирование, которые лежат в основе оптимизации многих параметров. Основная идея состоит в том, что вместо ручного вычисления производных и решения сложных уравнений, алгоритмы автоматически анализируют процесс вычисления функции и рассчитывают необходимые производные для нахождения оптимальных решений. Такой подход особенно полезен в задачах минимизации или максимизации функций, где нужно найти значения параметров, обеспечивающих наилучший результат. Например, в машинном обучении, когда модель обучается подстраиваться под данные путем минимизации функции ошибки. Здесь вычисление градиентов играет ключевую роль в алгоритмах оптимизации, таких как градиентный спуск.
Живой пример — преодоление препятствий с минимальным временем Представьте, что вам нужно быстрее всего добраться из точки А в точку Б по местности с разными типами поверхностей: например, по асфальту, песку и траве. Геометрия подсказывает, что самый короткий путь — это прямая линия. Но если на разных поверхностях вы движетесь с разной скоростью, оптимальный путь может стать гораздо более сложным. Пусть переходы между этими поверхностями задаются двумя точками пересечения, обозначим их как x1 и x2. Тогда общие затраты времени на прохождение пути описываются уравнением, учитывающим расстояния и скорости перемещения на разных типах поверхности.
Задача сводится к нахождению таких значений x1 и x2, при которых суммарное время будет минимальным. Ручные методы, предлагаемые в классической математике, заключаются в вычислении производных и решении системы уравнений, что может быть утомительно и сложно. Другой путь — перебор вариантов в поисках минимального значения, но это даст лишь приблизительный результат и потребует больших затрат времени. Дифференцируемое программирование предлагает решение, основанное на вычислении градиента функции и автоматическом улучшении параметров, что значительно ускоряет процесс и повышает точность. Инструменты нового поколения: JAX и автоматическое дифференцирование Одним из наиболее популярных и мощных инструментов для дифференцируемого программирования является библиотека JAX на языке Python.
JAX позволяет писать численные функции как обычно в Python, но при этом автоматически вычислять градиенты любой функции, не требуя дополнительных усилий по математическим вычислениям. Главная «магия» заключается в том, что JAX использует операторную перегрузку и цепное правило из математического анализа, строя граф вычислений функции и затем точно рассчитывая её производные. Благодаря этому появляется возможность быстро реализовывать алгоритмы, основанные на градиентном спуске — эффективном методе поиска минимума функций. Это открывает новые возможности практически для всех, кто работает с задачами оптимизации. Профессионалы смогут создавать сложные модели и быстро подстраивать параметры, а новички — освоить важные концепции без необходимости учить тонкости дифференцирования вручную.
Пример на практике — оптимизация пути движения Рассмотрим пример, который показывает, как можно использовать JAX для нахождения минимального времени прохождения маршрута с разными скоростями на участках. Сначала задаем фиксированные параметры: высота, расстояние и скорости движения на каждом типе поверхности. Затем определяем функцию, которая рассчитывает общее время прохождения на основе текущих значений точек пересечения x1 и x2. Используя функцию градиента от JAX, мы можем оценить, в каком направлении менять x1 и x2, чтобы уменьшить время. Затем с помощью цикла шаг за шагом корректируем значения, следуя отрицательному градиенту (поскольку задача — минимизация), пока не получаем оптимальные параметры.
В итоге компьютер быстро находит такой путь, который обеспечивает минимальное время преодоления. Как работает автоматическое дифференцирование? Возможно, у вас возникнет вопрос — а как именно JAX узнает, как вычислить производные, если мы пишем код как обычную функцию? Неужели это численное приближение или символическое вычисление, как в некоторых математических программах? Ответ: ни то, ни другое. JAX создает представление вычислений в форме графа, где каждый узел — это операция или переменная. Затем применяется цепное правило из анализа — один из фундаментальных принципов, позволяющий вычислять производные сложных составных функций, используя производные их составляющих. Этот метод позволяет вычислить точные производные с высокой скоростью и без ошибок приближений.
В результате, даже сложные вычисления, которые включают в себя возведение в степень, деление, функции тригонометрии и прочие операции, можно дифференцировать автоматически и эффективно. Преимущества и важные моменты Автоматическое вычисление производных сильно облегчает процесс оптимизации. Более того, оно позволяет интегрировать дифференцируемые компоненты с нейронными сетями, физическими моделями и другими сложными системами. Однако, необходимо помнить о некоторых нюансах. Для работы с произвольными типами данных и операциями применяется операторная перегрузка.
Многие стандартные операции и функции уже реализованы с поддержкой вычисления градиентов, но для некоторых нестандартных функций потребуется собственное определение, что может потребовать дополнительных усилий. Настройка параметров оптимизации, таких как шаг градиентного спуска и количество итераций, важна для достижения хороших результатов. Без оптимальной настройки алгоритм может либо застрять в локальном минимуме, либо медленно сходиться. Кроме того, вычисление градиентов требует дополнительного времени и памяти. При работе с очень большими задачами необходимо обращать внимание на производительность и, возможно, разбивать задачи на более мелкие части.
Расширенные возможности дифференцируемого программирования Помимо простых функций, современные дифференцируемые фреймворки позволяют дифференцировать вычисления, включающие ветвления, циклы и условия. Это значит, что вы можете создавать более сложные модели с условиями выбора и повторяющимися действиями, и все равно получать точные градиенты. Иногда нужно дифференцировать не только по параметрам, но и по самим условиям, определяющим ветвления. Для этого применяется метод, при котором обе ветви вычисляются одновременно с разными весами, отражающими вероятность их выбора. Это более сложный подход, но он расширяет возможности оптимизации в нелинейных и дискретных пространствах.
Интеграция с машинным обучением и нейронными сетями Дифференцируемое программирование прекрасно сочетается с обучением нейронных сетей. Библиотеки, такие как Flax для JAX, предоставляют средства для создания и обучения глубоких моделей с использованием тех же автоматических дифференциации и градиентных методов. Такой синтез позволяет строить физически информированные нейронные сети, комбинировать данные и знания физики для решения сложных задач, а также расширять методы оптимизации на область трехмерного моделирования, компьютерного зрения и других современных направлений. Современные дифференцируемые пакеты Сегодня существует большое количество специализированных пакетов и библиотек, которые реализуют дифференцируемые версии алгоритмов и операций в разнообразных сферах. К их числу относятся трехмерная визуализация, обработка изображений, аудио сигналов и многое другое.
Использование таких готовых решений позволяет создавать сложные пайплайны обработки и анализа данных, где можно эффективно оптимизировать компоненты на каждом этапе. Применение и перспективы дифференцируемого программирования Дифференцируемое программирование значительно расширяет круг задач, которые можно решать эффективно и автоматически. Еще несколько лет назад эта концепция применялась преимущественно в научных и инженерных расчетах, но стремительный рост Python-экосистемы и развитие мощных библиотек сделали ее доступной и для более широкой аудитории. В последние годы особенно заметен рост интереса к таким сферам, как дифференцируемый рендеринг и трехмерное моделирование, что становится возможным благодаря автоматическому вычислению градиентов в сложных системах. Технологии активно внедряются в стартапах и научных проектах, меняя подход к созданию визуального контента, робототехнике и научным симуляциям.
Для тех, кто стремится глубже погрузиться в тему, доступны учебные материалы, видеолекции и практические курсы, которые помогают освоить принципы автоматического дифференцирования и применение современных библиотек. Перспективы развития и расширения области дифференцируемого программирования выглядят многообещающими благодаря активному сообществу и постоянному появлению новых исследовательских и прикладных решений. Заключение Дифференцируемое программирование — мощный инструмент, который меняет подход к расчетам и оптимизации в науке и технологиях. Оно позволяет упростить работу с градиентами, ускорить создание оптимальных решений и расширить возможности разработки сложных моделей и алгоритмов. Благодаря таким библиотекам, как JAX, даже люди, не обладающие глубокими знаниями в математике, могут использовать силу дифференцирования для решения реальных задач.
Это открывает новые горизонты и перспективы для разработки инновационных систем во множестве областей, от робототехники и физики до компьютерной графики и машинного обучения.