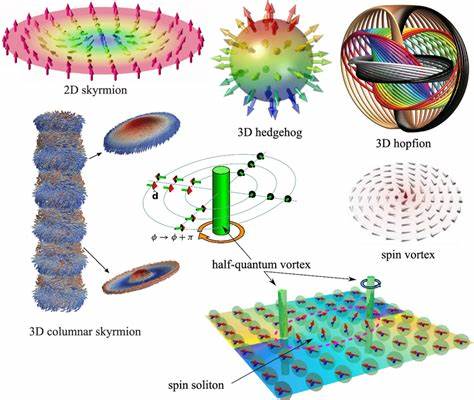
Современная физика материалов стремительно развивается в направлении глубокого понимания природы аморфных тел — структур, не обладающих долговременным порядком кристаллической решётки. Несмотря на широкое применение аморфных материалов в промышленности и науке, до сих пор существует значительный пробел в знании о том, что именно служит носителем пластических деформаций в этих системах. Традиционные подходы, основанные на представлении о дислокациях и других дефектах в кристаллах, не подходят для описания аморфных твердых тел из-за отсутствия трансляционной симметрии и долговременного структурного порядка. Именно здесь на сцену выходят концепции топологических дефектов, способные помочь в выявлении микроскопических областей, отвечающих за механическую нестабильность и пластичность. Особое место в данной тематике занимают ёжиковые (hedgehog) топологические дефекты — точечные особенности в векторных полях, характеризующие структуры, сходные по своей направленности с колючками ёжика, расходящимися радиально из одной точки.
Исследование таких дефектов в контексте трёхмерных аморфных материалов становится возможным благодаря новым методам анализа и мощным компьютерным симуляциям, как например, моделям Креймера-Греста, имитирующим поведение полимерных стекол в объёме. Одной из главных трудностей идентификации топологических дефектов в аморфных телах является отсутствие классической «подложки» с регулярной структурой, на которую бы можно было ориентироваться. Однако представление о топологии векторного поля, например, поля собственных векторов динамической матрицы или поля невязких смещений при деформациях, позволяет определить и классифицировать дефекты, не опираясь на упорядоченную решётку. В трёхмерном пространстве ёжиковые дефекты являются простейшим классом точечных дефектов, обладая топологической инвариантностью, которая сохраняется при непрерывных деформациях векторного поля. Важным аспектом является математическое описание этих дефектов через интеграйлы топологического заряда Q, который отражает число, характеризующее закрученность или направленность поля вокруг замкнутой поверхности.
Отличительной особенностью является то, что знак этого заряда в 3D, особенно для аморфных материалов, становится неоднозначным из-за особенностей симметрий поля. Поэтому для различения типов дефектов в дополнение к топологии используют геометрические характеристики, такие как анализ касательных 2D проекций и вычисление соответствующих завитков — в случае ёжиковых дефектов выделяют радиальные (monopole) и гиперболические (anti-monopole) структуры. Результаты численных исследований показывают, что количество таких дефектов в собственных векторных полях трёхмерных аморфных тел концентрационно коррелирует с фоном низкочастотных вибрационных состояний и демонстрирует масштабирующее поведение, аналогичное закону Дебая. Более того, территория локализации этих дефектов совпадает с областью так называемых мягких пятен — зон с высокой склонностью к структурным перестройкам и пластичности. Особое внимание уделяется гиперболическим ёжиковым дефектам, которые проявляют повышенную корреляцию с зонами пластичности.
Это согласуется с наблюдениями в двухмерных стеклах, где дефекты с отрицательным топологическим зарядом и характерной анти-вихревой геометриейчувствительнее откликаются на внешние нагрузки и провоцируют структурные сдвиги. Следовательно, именно геометрические, а не только топологические параметры дефектов служат ключом к пониманию природы и локализации пластических событий в материалах без упорядоченности. Интересно, что анализ топологических дефектов в полях смещений, возникающих при аффинных и неаффинных деформациях, даёт даже более явную связь с маломасштабными структурными преобразованиями, чем изучение собственных векторов малых возбуждений. В связи с этим существует перспективы применения подобных подходов в экспериментальной физике, где напрямую регистрируются смещения молекул или частиц, особенно в трехмерных коллоидных или гранулярных системах. Важный вклад в теорию вносит также понимание механизмов взаимодействия и взаимного расположения ёжиковых дефектов, которые склонны образовывать пары с антиположительными зарядами и, возможно, кластеры, минимизируя локальный топологический заряд.
Данная тенденция сказывается на макроскопических свойствах материала, способствуя появлению пластических зон с устойчивой геометрической структурой. Существует несколько перспективных направлений дальнейших исследований. Во-первых, необходимо развивать теоретическую базу, которая бы позволила связать топологические и геометрические характеристики с физической динамикой дефектов в процессе деформации. Во-вторых, интересен вопрос влияния химического состава, взаимодествия между молекулами и их структурной организации на появление и эволюцию ёжиковых дефектов. В-третьих, экспериментальные методы визуализации и анализа трёхмерной динамики аморфных систем должны быть дополнены возможностями обнаружения и классификации топологических дефектов.
В конечном счёте, интеграция топологических методов в науку об аморфных материалах открывает перспективу создания новых инструментов прогнозирования и контроля их механического поведения. Ёжиковые дефекты в 3D аморфных телах становятся не только абстрактным математическим понятием, а реально измеримыми и управляющими элементами, дающими представление о внутренней сложнейшей структуре стекол и полимерных стеклообразующих систем. Это фундаментальный шаг к более точной инженерии материалов следующего поколения, обладающих высокими регуляруемыми прочностными и пластичными свойствами. Углубленное исследование связи между геометрией и топологией ёжиковых дефектов за пределами двумерных моделей позволяет выходить на новый уровень понимания процессов пластического разрушения и переупорядочения в аморфных и дисордерных твердых веществах. Современные симуляционные методики и концепции топологической физики применительно к 3D аморфным структурам формируют уникальные возможности выявления скрытой внутренней организации и предсказания критических состояний материалов, что невозможно традиционными подходами.
Таким образом, ёжиковые топологические дефекты представляют собой мост между абстрактной математикой и конкретными физическими процессами, проявляющимися в реальных материалах. Их изучение способствует развитию комплексного представления о пластичности и механической стабильности трёхмерных аморфных тел, что имеет огромное значение для материаловедения, инженерии и прикладной физики.