Современная космологическая гидродинамика является одной из ключевых областей астрофизики, направленной на исследование формирования и эволюции структуры Вселенной, включая галактики, скопления и крупномасштабную структуру. Для глубокого понимания этих процессов учёные активно используют численные методы, позволяющие смоделировать сложные взаимодействия газа, тёмной материи и гравитации в масштабах миллионов и миллиардов световых лет. Однако традиционные подходы к гидродинамическому моделированию имеют свои ограничения и недостатки, что затрудняет получение адекватных и достоверных результатов. В свете этого особый интерес представляет инновационный метод, основанный на использовании движущейся сетки со свойствами Галиилеевой инвариантности, предложенный Волкером Спрингелем и реализованный в коде AREPO. Этот метод позволяет преодолеть многие проблемы классических техник и открывает новые возможности в исследовании космологической гидродинамики.
Для начала важно разобраться в том, какие ключевые методы гидродинамического моделирования применяются сегодня и в чём их основные ограничения. Наиболее распространены два подхода: лагранжевский метод — сглаженная частицная гидродинамика (SPH), и эйлеровский метод с использованием фиксированной квадратной сетки, зачастую с адаптивным уточнением ячеек (AMR). SPH характеризуется тем, что пространство заполняется набором частиц, движущихся вместе с потоком, что даёт хорошие результаты при моделировании сжимаемых форм жидкости и облегчает адаптацию пространственного разрешения к локальным требованиям. Однако этот подход зачастую переоценивает стабильность интерфейсов между потоками, подавляя развитие гидродинамических нестабильностей, таких как, например, нестабильность Кельвина–Гельмгольца. С другой стороны, эйлеровские методы на фиксированных каркасных сетках отличаются высоким качеством воспроизведения ударных волн и резких переходов, но испытывают проблемы с сохранением инвариантности относительно перевода системы отсчёта — так называемой Галиилеевой инвариантности.
В условиях космологии, где течение газа часто имеет высокоскоростные крупномасштабные потоки, нехватка этой инвариантности приводит к численной диффузии, искажению результатов и чрезмерному перемешиванию вещества, что ухудшает точность моделирования. В своём исследовании Волкер Спрингель предлагает уникальный гибридный метод, который объединяет преимущества как лагранжевых, так и эйлеровских подходов. Центральная идея заключается в использовании движущейся неструктурированной сетки, основанной на Вороного-тесселляции, — разбиении пространства на полиэдры, каждый из которых соответствует одной сеточной точке. Особенность этого подхода в том, что точки, создающие Вороного-клетки, могут двигаться вместе с локальным газовым потоком. Таким образом достигается лоранжева динамика, но при этом сеть сохраняет гибкую структуру, позволяющую избежать её искажения и обеспечить точное решение уравнений гидродинамики при помощи консервативных численных схем.
Метод предлагает решение гиперболических уравнений идеальной гидродинамики с помощью подхода конечных объёмов второго порядка точности, основанного на полноразмерном решении римановской задачи. Такая высокая точность схемы позволяет адекватно моделировать сложные процессы, включая сформирование ударных волн, контактов и нестабильностей в газе. Когда точки передвигаются по заблаговременно определённым траекториям, сохраняется полная Галиилева инвариантность: результаты моделирования не зависят от равномерного добавления скорости ко всем компонентам системы. Реализация этого метода заняла значительный объём работы, учитывая потребности параллельной обработки данных на современных вычислительных кластерах и необходимость адаптивного увеличения или уменьшения разрешающей способности сетки в зависимости от локальных физических условий. Обработка гравитационного взаимодействия с тёмной материей и газом осуществляется эффективно, позволяя объединить высокоточное гидродинамическое моделирование с динамикой частиц без ущерба производительности.
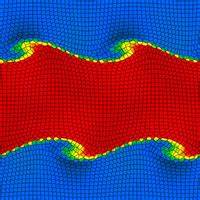
Преимущества этого подхода особенно заметны при моделировании процессов, связанных с развитием гидродинамических нестабильностей. Традиционные SPH-методы часто преуменьшают влияние таких явлений, подавляя развитие турбулентных структур и перемешивания веществ. Новый движущийся сеточный метод способен точно воспроизвести эти явления, демонстрируя более реалистичное поведение потоков, что особенно важно при исследовании смешивания газов в галактических ветрах и взаимодействиях между различными структурами. Кроме того, автоматическая адаптация разрешения сетки решает проблему эффективного использования вычислительных ресурсов, повышая детализацию в тех областях, где происходят важные физические процессы, и снижая её в менее значимых регионах. Это позволяет выполнять масштабные вычисления с высоким качеством, не расходуя излишне вычислительные мощности.
В серии тестовых задач разработчики подтвердили успешность и стабильность метода на примерах классических тестовых проблем гидродинамики: взрывных волн (проблема Седова-Тейлора), нестабильностей Релея–Тейлора и Кельвина–Гельмгольца, ротирующих дисков и др. Визуализации и динамические видео, полученные с помощью кода AREPO, демонстрируют плавность и реалистичность течений, что является убедительным доказательством преимуществ метода перед традиционными подходами. Инновации, которые вносит этот метод, имеют большое значение для космологии, особенно при моделировании формирования галактик и крупномасштабных структур. Развитие точных моделей гидродинамики в контексте расширяющейся Вселенной позволяет более корректно учитывать механизмы охлаждения газа, образование звёзд и обратное влияние звёздных ветров и активных ядер на окружающую среду. Всё это способствует улучшению согласования теоретических моделей с астрономическими наблюдениями мира на самых разных масштабах.
Будущее этой методики выглядит многообещающе, поскольку её гибкая архитектура позволяет интегрировать дополнительные физические процессы — магнетогидродинамику, релятивистские эффекты, взаимодействия с радиацией — без существенного усложнения алгоритмов. Это открывает путь к созданию универсальных и высокоточных космологических симуляторов, способных раскрывать тайны происхождения структуры и эволюции Вселенной. В заключение стоит подчеркнуть, что применение галиилеево-инвариантных гидродинамических симуляций на движущейся сетке представляет собой качественный скачок в области численных методов астрофизики. Совмещая лучшие качества существующих методов и преодолевая их ограничения, эта инновация способствует более глубокому и точному пониманию природных процессов, формирующих космос, и служит мощным инструментом для исследователей по всему миру, стремящихся разгадать сложнейшие загадки Вселенной.