В современном программировании стремление к оптимизации кода является неизменным приоритетом для разработчиков, компиляторов и исследователей. Среди множества подходов, направленных на улучшение производительности программ и упрощение выражений, особое место занимает концепция, известная как Equality Saturation. Этот мощный метод позволяет выполнять глобальную оптимизацию выражений, раскрывая скрытые равенства и обеспечивая обширные варианты переписывания для достижения оптимальных результатов. Понимание Equality Saturation начинается с представления о том, как современные компиляторы и оптимизаторы работают с выражениями. Традиционные методы оптимизации часто базируются на последовательном применении правил переписывания, при этом каждая трансформация применяется к текущему виду выражения.
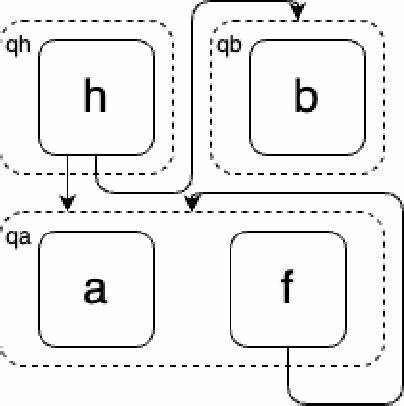
Однако такой способ может привести к выбору локально оптимальных, но не оптимальных в глобальном смысле выражений, поскольку каждое переписывание влияет на последующие. Equality Saturation предлагает иную парадигму. В ее основе лежит структура данных, называемая e-graph (эквивалентный граф), который одновременно хранит широкое множество выражений, относящихся к одному и тому же значению, объединяя их в эквивалентные классы. Таким образом, оптимизатор не просто трансформирует выражение шаг за шагом, а накапливает все возможные варианты его эквивалентных форм. Основная идея заключается в том, чтобы "наполнить" e-graph всеми возможными эквивалентными выражениями, используя набор правил переписывания.
Каждое правило содержит шаблон, согласно которому одна конструкция может быть преобразована в другую без изменения семантики программы. Такие правила включают коммутативность и ассоциативность операций, константное вычисление и многие другие. Применение этих правил происходит итеративно. Система находит все совпадения шаблонов в графе и расширяет его новыми эквивалентными выражениями. Постепенно e-graph насыщается, содержащий в себе обширный набор вариантов.
Это затрудняет классическую проблему оптимизации, где увеличивается объем вычислений, но благодаря эффективным алгоритмам и структурам данных процесс остается управляемым. Значительный плюс подхода заключается в возможности последующей выборки наилучшего по определенной метрике выражения из множества, что ускоряет поиск оптимальных решений. Метрики могут быть разнообразными: минимизация количества операций, снижение использования памяти, упрощение кода и даже учет специфики аппаратных платформ. Соединяя теорию и практику, важным примером применения Equality Saturation является оптимизация выражений линейной алгебры и арифметики, где часто встречаются подобные правила, как коммутативность сложения и умножения, ассоциативность, дистрибутивные свойства и константные подстановки. Здесь через расширенный e-graph можно не только упростить выражение, но и выполнить факторизацию, повысив эффективность вычислений.
При реализации Equality Saturation складывается задача разработки DSL (Domain Specific Language) для определения выражений и правил переписывания. В языках, поддерживающих operator overloading и возможность интроспекции, таких как Python с некоторыми библиотеками, можно элегантно описывать эти правила, делая инструментарий удобным для применения в самых разных задачах. Одной из сложностей применения метода является контроль роста e-graph, так как добавление каждого нового выражения в эквивалентный класс увеличивает размер графа. Для борьбы с этим применяются различные эвристики, ограничивающие глубину поиска, использование специальных структур хранения и периодическая "перегруппировка" и слияние эквивалентных классов. Область применения Equality Saturation широка.
Помимо компиляторной оптимизации, метод находит место в автоматическом доказательстве теорем, оптимизации запросов к базам данных, генерации и упрощении машинного кода, а также в области машинного обучения и программного анализа. В научно-исследовательском сообществе этот метод вызывает большой интерес, поскольку сочетает в себе эффективный механизм поиска и глубокий семантический анализ выражений. Он превосходит классические методы переписывания за счет параллельного поддержания множества вариантов, позволяя находить неожидано оптимальные преобразования. Практическая реализация Equality Saturation включает регистрацию правил, которые формализуют свойства операций и вычислений. К примеру, коммутативность сложения записывается как правило, согласно которому выражение "x + y" эквивалентно "y + x".
Аналогично определяются правила ассоциативности и константного вычисления. Для запуска оптимизации правила применяются итерационно несколько раз, постепенно насыщая e-graph. Результатом работы оптимизатора становится e-graph, в котором представлено множество эквивалентных форм изначального выражения. Механизм извлечения выбирает из этого множества наилучший вариант по заданной метрике. Таким образом, достигается более высокий уровень оптимизации, чем при традиционном последовательном переписывании.
В контексте современных вычислительных задач, где оптимизация играет ключевую роль для повышения производительности и снижения энергопотребления, Equality Saturation демонстрирует высокую практическую ценность. Инструменты, основанные на этом методе, помогают разработчикам создавать код, максимально приближенный к теоретически оптимальным решениям. В заключение, Equality Saturation - это инновационный и эффективный метод оптимизации программных выражений, который ведет себя как глобальный расширитель пространства эквивалентных форм, обеспечивая качественно новый уровень анализа и трансформации кода. Понимание и внедрение этого подхода открывает новые возможности для разработки быстрых, компактных и эффективных программных систем. .