Первая главная компонента — один из основополагающих инструментов в области анализа данных и компьютерной графики. Она определяет направление наибольшего разброса точек в многомерном пространстве и находит применение в таких задачах, как цветовая квантования, сжатие текстур и построение ориентированных ограничивающих объемов для 3D-моделей. Однако классический метод вычисления первой главной компоненты требует значительных ресурсов из-за необходимости вычисления ковариационной матрицы и извлечения собственных векторов. В этом контексте аппроксимация первой главной компоненты становится привлекательным компромиссом между быстродействием и точностью. Приближенный метод, вдохновленный реализацией из библиотеки exoquant, предлагает простой и эффективный способ нахождения вектора максимальной варьирующейся компонентности без необходимости сложных вычислений.
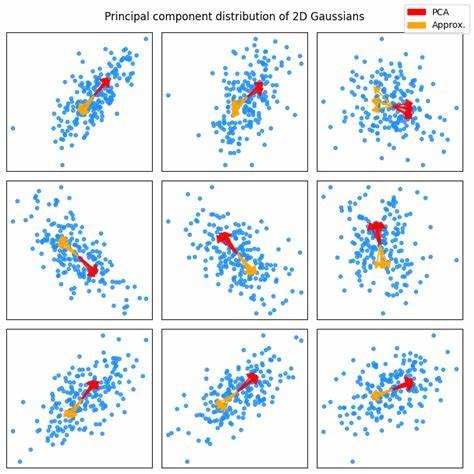
Суть метода заключается в последовательном суммировании направлений отклонений точек от среднего значения с условием, что направление каждого добавляемого вектора согласовано с текущим вектором направления. Такая процедура также требует предварительного упорядочивания данных по оси с максимальной дисперсией для обеспечения определенности результатов. Особенностью данного подхода является его простота в реализации: достаточно вычислить среднее значение данных, оценить дисперсию по каждой оси, отсортировать точки, а затем пройтись циклом по точкам, аккумулируя вектор отклонений с корректировкой направления. По окончании вычисляется нормализованный вектор, который служит приближением к первой главной компоненте. Эксперименты с использованием двумерных гауссовских распределений показали, что такой метод выдает результаты, близкие к классическому PCA, особенно при низком уровне шума.
Это открывает широкие возможности для применения в графических движках и библиотеках, где важна скорость и экономия ресурсов. Однако стоит учитывать, что метод имеет свои ограничения. Если данные имеют сложную структуру, например, содержат несвязанные разноосные распределения, аппроксимация может давать некорректные результаты. Иллюстрацией служит пример с точками, равномерно распределенными по двум осям, где классическое PCA точно выявляет главную ось вариации, а приближённый метод ошибается в направлении. Несмотря на это, для множества практических задач, связанных с натуральными изображениями и текстурами, приближенный метод показывает достойную устойчивость и дает качественные результаты.
Важно отметить, что данный подход снижает вероятность возникновения критических ошибок по сравнению с полностью «грубыми» методами, которые просто используют разброс по осям без учета корреляций. К тому же его реализация требует меньше вычислительных ресурсов, что критично для систем с ограниченными возможностями или при работе с большими объемами данных. Рассматриваемая реализация на Python с использованием библиотеки NumPy позволяет быстро протестировать метод и интегрировать его в исследовательские и прикладные проекты. На практике шаг сортировки по оси максимальной дисперсии оказывается важным для детерминированного результата и некоторого улучшения точности аппроксимации. Наблюдается, что выходной вектор в таком случае оказывается направленным преимущественно в сторону отрицательных значений по оси с максимальным разбросом, что не влияет на качество интерпретации главной компоненты, поскольку направление вектора асимметрично.
Метод также был успешно применен для построения ориентированных ограничивающих объемов (OBB) на основе основного направления вариации. В таких задачах комплексный анализ главной компоненты обычно требует вычисления полного ортонормального базиса. Но приближенная первая главная компонента вместе с алгоритмами построения ортогональных векторов, такими как предложенный Дюффом и соавторами метод, позволяют эффективно и достаточно точно определять ограничивающие конструкции, что важно для оптимизации графических движков и ускорения обработки 3D-моделей. Исторический контекст разработки этого метода восходит к реализации exoquant из 2004 года, которая использовалась для цветовой квантования, где баланс между качеством и скоростью обработки имеет первостепенное значение. Ее современный перевод и эксперименты в различных окружениях подтверждают устойчивость и практичность подхода.
Для профессионалов, работающих с анализом изображений, визуализацией и машиностным обучением, понимание данной аппроксимации расширяет инструментарий и позволяет выбирать оптимальные решения в зависимости от требований по точности и скорости. Следует отметить, что приближенный метод является частным случаем инкрементального PCA — класса алгоритмов, которые обновляют оценки главных компонент по мере увеличения объема данных без необходимости повторного полного расчета. Это делает подход востребованным в условиях стриминговых данных и онлайн-аналитики. В завершение, приближенное вычисление первой главной компоненты представляет собой полезный компромисс, объединяющий простоту реализации и высокую эффективность, что особенно актуально в компьютерной графике и задачах обработки цвета. Несмотря на ограничения в сложных распределениях, метод отлично справляется с естественными наборами данных и открывает перспективы для оптимизации многих современных алгоритмов.
Постоянные эксперименты и улучшения помогут адаптировать данную технику под разные сценарии, расширяя ее применение и повышая качество графических и визуальных решений.