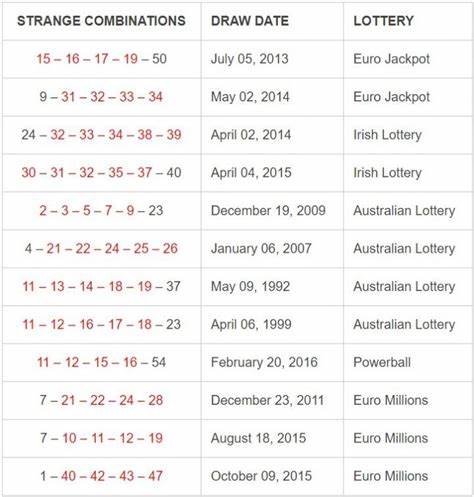
Лотерея с её обещанием быстрых и крупных выигрышей всегда привлекала внимание миллионов людей по всему миру. Кто не мечтал сорвать джекпот и изменить свою жизнь в одно мгновение? Однако для большинства участников шанс успеха крайне невелик — в традиционных лотереях выигрыш зависит исключительно от удачи и случайного выбора чисел. Но существует ли способ гарантированно выиграть? Математика утверждает, что да, при условии значительных вложений и правильного подхода. Разберём, почему и как это возможно с помощью комбинаторики и стратегии объединения ресурсов.Лотерея — это игра на вероятности, а точнее, на комбинаторных вычислениях.
К примеру, известная американская игра Powerball требует участника выбрать пять белых шаров из диапазона от 1 до 69 и один красный шар из 26 возможных. Комбинаторика помогает определить общее количество уникальных вариантов таких комбинаций, то есть общее количество возможных билетов. Эта цифра колоссальна: миллионы вариантов, что объясняет невероятно низкие шансы на победу при покупке одного или нескольких билетов.В теории, чтобы гарантированно выиграть, нужно купить билет с каждой возможной комбинацией. Таким образом, вы наверняка окажетесь обладателем выигрышного номера.
Звучит просто, но практически выполнить такую стратегию крайне сложно из-за огромного количества вариантов и соответствующих финансовых затрат. Однако именно эта идея — основа так называемой безусловной гарантии выигрыша с точки зрения математики.Для примера в Powerball потребуется приобрести все возможные варианты комбинаций, что потребует огромных средств. Чем больше диапазон выбираемых чисел и чем больше количество выбираемых шаров, тем выше цена подобной стратегии. Именно по этой причине авторы, исследующие данный вопрос, подчёркивают, что для реализации этой стратегии необходимо либо уже иметь значительные финансовые ресурсы, либо объединиться в крупные группы участников, которые смогут совместно инвестировать крупную сумму в покупку всех или почти всех возможных комбинаций.
Объединённые команды игроков, часто называемые синдикатами, уже сейчас практикуют данный подход. Объединив деньги, они покупают большое количество билетов с уникальными номерами, значительно повышая свои шансы на выигрыш. Несмотря на то, что синдикаты сами по себе не гарантируют стопроцентный выигрыш, они существенно повышают вероятность успеха по сравнению с индивидуальными игроками.Комбинаторная формула, используемая для подсчёта количества билетов, включает факториалы и биномиальные коэффициенты и является фундаментом для понимания структуры всех возможных комбинаций. Именно от этого зависит размер необходимого бюджета для гарантированного покрытия всех вариантов.
Интересный факт заключается в том, что в ряде случаев сумма потенциального выигрыша достигает или превышает совокупный бюджет, необходимый для покупки всех вариантов билетов. Однако стоит учитывать, что при таком подходе выигрыш придётся делить на множество участников, если джекпот делят между несколькими победителями, а также вероятны дополнительные сложности, такие как невозможность оперативно купить такие огромные партии билетов из-за организационных или правовых ограничений участников лотерей.Изучая лотерейные игры с математической точки зрения, важно также учитывать дополнительные факторы, например вероятность появления повторяющихся номеров, правила лотереи и ее особенности. Некоторые игры позволяют выбрать один и тот же номер в разных частях билета, что потенциально увеличивает сложность подсчёта всех вариантов.В теории, любой, у кого есть достаточно ресурсов, может использовать чистую комбинаторику для покрывания полностью пространства всех комбинаций и таким образом гарантировать себе джекпот.
Но на практике размер ставок и организационные моменты делают подобную операцию доступной лишь элите. Это также объясняет, почему большинство простых игроков продолжают полагаться на удачу и интуицию при выборе чисел.Тем не менее, понимание базовой теории комбинаторики и вероятностей важно для любого, кто хочет серьёзно подходить к игре в лотерею. Это помогает лучше осознать, каковы реальные шансы на победу, и принимать более взвешенные решения о расходах на участие. Лотерея — это в первую очередь азартная игра, а математика позволяет лишь просчитать шансы, но не изменить случай.