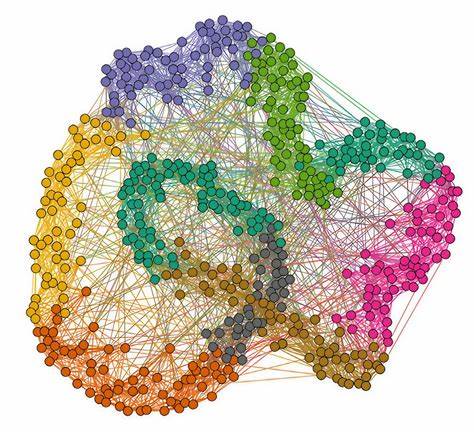
Теория графов — уникальная и мощная ветвь математики, которая изучает объекты и связи между ними, формируя абстрактные модели, называемые графами. Несмотря на глубокую абстрактность, эта область оказывает огромное влияние на множество дисциплин и решает практические задачи, которые касаются повседневной жизни, технологий и научных открытий. Истоки теории графов уходят в XVIII век, когда знаменитый математик Леонард Эйлер решил задачу о семи мостах Конigsберга. Горожане пытались пройти по мостам так, чтобы пройти каждый ровно один раз, но никто не мог доказать, возможно ли это. Эйлер перевел эту проблему в математическую форму, заменив острова точками — вершинами, а мосты — линиями, соединяющими их, то есть ребрами графа.
Благодаря этому он доказал, что решение невозможно, и тем самым положил начало новой области науки — теории графов. Современный мир постоянно усложняется, сети становятся все более запутанными и взаимосвязанными. Теория графов предоставляет инструменты, позволяющие анализировать структуры социальных сетей, маршрутов транспортных систем, генетических взаимодействий, компьютерных алгоритмов и многих других систем. Исследования в этой области не только способствуют развитию математики, но и формируют основы для инновационных решений в различных сферах. Примером значимого прогресса в теории графов является работа математиков, таких как Мария Чудновски из Принстонского университета.
Ее вклад в решение так называемой проблемы совершенных графов спустя почти полвека после выдвижения гипотезы является признанным научным достижением. Совершенные графы — это особый вид графов, где минимальное число цветов, необходимых для раскраски вершин так, чтобы соседние вершины отличались цветом, совпадает с размером наибольшей связной группы вершин, называемой кликой. Такая характеристика облегчает решение многих алгоритмических задач, связанных с упорядочиванием и классификацией объектов. Графы позволяют решать практические проблемы, например, планирование рассадки гостей на свадьбе. Если представить каждого гостя как вершину, а связь между ними, которая может означать неприязнь или конфликт, как ребро, становится возможным с помощью алгоритмов раскраски графа распределить гостей по столам так, чтобы никакие «враждебные» пары не оказались рядом.
Это упрощение реальной социальной задачи с помощью математического подхода иллюстрирует универсальность теории графов. Широкое применение теория графов находит в информатике. Алгоритмы поиска оптимальных маршрутов, организации данных, обработки социальных сетей и построения эффективных коммуникационных систем — все это связано с моделированием и изучением графов. Особенно актуальны их применения в эпоху больших данных, где анализ сложных сетей и взаимосвязей становится ключевым для понимания информации. Также нельзя не отметить вклад теории графов в биологию.
Моделирование сетей взаимодействий между белками, генами или видами в экосистемах помогает понять более глубокие процессы жизни и способствует развитию биоинформатики и системной биологии. Это дает возможность предсказывать поведение сложных биологических систем и ускоряет разработку новых методов лечения и диагностики. Еще одна масштабная задача — анализ городских и транспортных сетей. Используя графы, можно оптимизировать движение транспорта, распределение ресурсов, проектирование сетей электроснабжения и связи. В технике теория графов помогает решать задачи маршрутизации в коммуникационных сетях, повышая их устойчивость и эффективность.
Интересно, что теория графов транснациональна и не имеет языковых барьеров. Математика как универсальный язык, связывает ученых разных стран и культур, создавая общую основу для сотрудничества и накопления знаний. Математические доказательства и алгоритмы, разработанные в одном уголке мира, могут мгновенно стать достоянием всего научного сообщества. Помимо практических применений, теория графов развивает навык ясного и структурированного мышления. Математики, работающие в этой области, учатся разбивать сложные системы на части, выявлять важное и игнорировать несущественное, что полезно не только в науке, но и в повседневной жизни.
Сегодня теория графов остается динамично развивающейся областью с множеством нерешенных задач и гипотез, стимулируя активные исследования. Новые открытия открывают возможности для создания эффективных алгоритмических решений и способствуют пониманию сложных систем, значительно меняя способы взаимодействия человека с окружающим миром. Таким образом, теория графов не просто абстрактное математическое направление, а живой и важный инструмент, который помогает разрабатывать решения, улучшать технологии и расширять наше понимание сложных взаимосвязей в самой разной области — от повседневных социальных ситуаций до глобальных научных и технических вызовов.