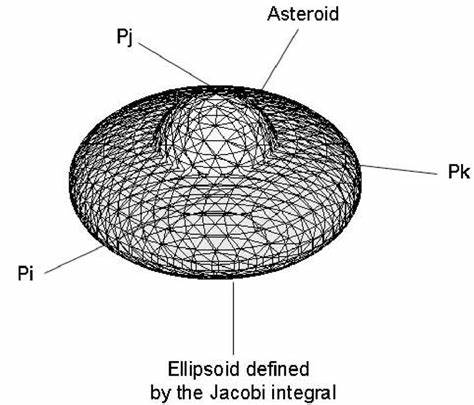
Эллипсоид Якоби представляет собой триосный эллипсоид, находящийся в состоянии гидростатического равновесия, которое формируется вследствие вращения самогравитирующегося тела с постоянной угловой скоростью. Эта форма равновесия получила свое название в честь немецкого математика Карла Густава Якоби, внесшего фундаментальный вклад в изучение подобных фигур. Эллипсоид Якоби занимает особое место в астрономии и физике, так как описывает поведение вращающихся массивных объектов, состоящих из жидкости с однородной плотностью, как, например, некоторые астероиды, планеты или даже карликовые планеты, обладающие значительной скоростью вращения и следовательно отклоняющиеся от простой сферической формы. Исторически до открытия эллипсоида Якоби считалось, что единственной фигурой равновесия для вращающегося гравитационно-сжимаемого тела является сфероид Маклорена, открытый ещё в XVIII веке и характеризующийся особыми свойствами вращающегося тела с двумя равными полярными осями. Исследования Лагранжа в начале XIX века допускали возможность существования триосных эллипсоидов, но при этом он предполагал, что две оси экваториального сечения должны быть равны, возвращая к решению маклореновского сфероида.
На этом фоне открытия Якоби в 1834 году имели революционный характер, так как он продемонстрировал, что равновесие возможно и для эллипсоида с полностью различными тремя полуосями. Суть открытия заключалась в том, что вращение тела может способствовать формированию более сложных форм, отличающихся от сфероида с двумя равными осями, таким образом расширяя теорию фигур равновесия для гравитационных тел. Математическая модель эллипсоида Якоби базируется на вычислении угловой скорости вращения около полярной оси с учётом влияния трёх полуосей, обозначаемых как a, b и c, где a и b соответствуют полуосям экваториального сечения, а c – полярной полуоси. Ключевым условием является постоянство объёма тела, что обозначается произведением abc равным постоянной величине. Формула угловой скорости вращения включает интегралы, выражаемые через эллиптические интегралы, подробно учитывающие взаимное влияние всех трёх полуосей и распределение плотности тела.
Эта теория даёт возможность определить диапазон значений для полуосей, в рамках которого тело сохраняет равновесие, например, существует неравенство, связанное с их величинами, необходимое для устойчивости. Особое значение имеет интеграция с учётом плотности тела и гравитационной постоянной, благодаря чему можно предсказывать динамические и устойчивостные состояния в зависимости от скорости вращения. Помимо чисто теоретических аспектов, эллипсоид Якоби тесно связан с другими фигурами равновесия, такими как эллипсоид Дедекинда. Если эллипсоид Якоби описывает тело, вращающееся как жёсткое тело без внутреннего течения жидкости в системе, то эллипсоид Дедекинда характеризует тело с постоянным направлением в пространстве, внутри которого жидкость совершает циркуляцию, при этом внешних вращений может не наблюдаться. Это демонстрирует сложность и разнообразие физических состояний, при которых гравитирующие жидкости могут находиться в равновесии и иллюстрирует глубину взаимодействий между кинематикой и внутренними потоками.
Для каждого эллипсоида Якоби существует соответствующий эллипсоид Дедекинда с идентичными полуосями и массой, но отличающимся распределением скоростей внутри тела, что подчёркивает богатую структуру движения и эволюцию вращающихся масс. Наука о вращающихся эллипсоидах имеет практическую важность в астрофизике и планетологии, ведь многие небесные тела, включая некоторые карликовые планеты и астероиды, приобретают формы, близкие к трёхосным эллипсоидам в силу своей быстрой скорости вращения и жидкой, или частично жидкой, внутренней структуры. Например, карликовая планета Хаумеа демонстрирует форму эллипсоида Якоби, что позволяет физикам более точно оценить её внутренние параметры, динамику и эволюционную историю. Становится понятным, что фундаментальная теория, разработанная более полутора веков назад, оказывает прямое влияние на современные исследования космических объектов. Более того, формулы Якоби лежат в основе численных моделей и симуляций, позволяя исследовать не только равновесные состояния, но и динамику переходов между формами, например, от маклореновского сфероида к эллипсоиду Якоби при определённых условиях вращения и потерь энергии в системе.
Важным аспектом является рассмотрение устойчивости данных фигур, где маклореновский сфероид может быть динамически устойчив, но не устойчив относительно медленных изменений (секулярная устойчивость), что приводит к постепенному переходу к форме эллипсоида Якоби, если присутствует вязкий компонент жидкости, способный рассеивает энергию. Математическая строгость и физическая интуиция, объединённые в формулировках Якоби, позволяют глубже понять разнообразие возможных состояний вращающихся гравитирующих тел, что способствует развитию науки в области небесной механики и динамики жидкостей. Эллипсоиды Якоби рассматриваются в контексте более широкого класса фигур равновесия, к которым относятся сфероиды Маклорена, эллипсоиды Дедекинда, а также фигуры Римана и Роша. Каждая из этих форм играет свою роль в описании реального поведения небесных и физических объектов при различных условиях плотности, скорости вращения и внутреннего строения. В математическом плане теорема Якоби разрушила устоявшееся первоначальное представление об исключительности сфероидов вращения и открыла целое направление исследований, связанные с устойчивостью и формами вращающихся жидкостных масс.
Исторические работы Якоби, а также дальнейшие исследования физиков и астрономов свидетельствуют о том, как тесно связаны фундаментальные математические исследования и их применение к задачам реальной физики и астрономии. В современных условиях количество данных о вращающихся неупругих и сжимаемых объектах в космическом масштабе постоянно растёт, благодаря космическим миссиям, наблюдениям и компьютерному моделированию. Это вновь подчёркивает актуальность классических формул и моделей Якоби на новом этапе развития науки. Изучение эллипсоида Якоби продолжает приносить инсайты в области формирования и эволюции планетарных тел, изучения коллапса газовых облаков и процессов внутренней динамики звёзд. Применение этих знаний также расширяется на инженерные и прикладные отрасли, где моделируется поведение вращающихся жидкостей и тел сложной формы.
В итоге, эллипсоид Якоби остаётся ярким примером синтеза математики, физики и астрономии, открывая окно в сложный и красивый мир вращающихся небесных тел, их форм и динамических свойств.