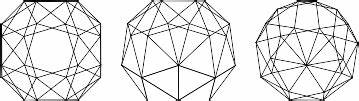
Многогранники - одни из самых увлекательных и изучаемых объектов в математике и геометрии. Среди них особое место занимает Рупертова сфабрикованная куба - фигура с удивительными свойствами и историей, которая привлекает внимание как ученых, так и любителей головоломок по всему миру. Этот объект, вместе с другими "математическими дырами" и формами, открывает захватывающие перспективы для исследования пространства и симметрии, а также вдохновляет на новые открытия в области теории многогранников. Рупертова сфабрикованная куба возникает из классического куба, но отличается своей способностью во внутрь вписать копию самого себя - то есть из большого куба можно вырезать меньший куб, который можно без повреждений извлечь и, что более удивительно, поместить обратно. Это свойство кажется невозможным на первый взгляд, но детальный анализ и построение моделей показывают, что самодополняющиеся свойства относятся к более широкой группе фигур, известной как "математические дыры".
Эти дыры - особые пространства внутри многогранников, которые позволяют создавать неожиданные взаимодействия между поверхностями и объемом. Исследование Рупертова сфабрикованного куба включает как классические методы геометрии, так и современные компьютерные технологии. Благодаря 3D-моделированию и численным методам удалось получить более точное представление о параметрах, необходимых для создания такой фигуры, а также проверить корректность решений, основанных на теоретических выкладках. Помимо куба, математическая литература и прикладные исследования богаты примерами других многогранных форм, обладающих уникальными свойствами. Среди них особую значимость приобретают тела Архимеда, Платоновы и Каталановы многогранники, каждое из которых представляет собой гармоничное сочетание симметрии и сложности.
Четкое понимание их структуры и взаимосвязей помогает раскрыть новые закономерности и улучшить математическую интуицию в области топологии и пространственной геометрии. Среди последних разработок стоит отметить работу, представленную на конференциях исследователями, специализирующимися на формальных доказательствах и верификации геометрических гипотез. Такие проекты сочетают художественный подход визуализации с серьезным инструментарием математической логики, что расширяет горизонты по созданию надежных и воспроизводимых моделей. Например, формальная проверка решения, связанного с трииакис тетраэдром, показала, как аккуратное использование вычислительных средств помогает устранять недочеты и повышать степень достоверности предложенных теорий. Любители головоломок и интерактивных задач также найдут интерес в видеоигровых версиях, разработанных с намерением усложнить и разнообразить процесс изучения многогранников.
Такие проекты, несмотря на игровую оболочку, зачастую требуют глубокого понимания геометрических принципов и стимулируют когнитивное развитие, усиливая взаимосвязь между обучением и развлечением. Современные технологии позволяют создавать интерфейсы, где можно вращать, трансформировать и комбинировать фигуры, что способствует освоению сложных понятий в интуитивной форме. На фоне постоянного развития программного обеспечения и доступности мощных компьютеров органы исследований облегчают процесс создания трехмерных моделей. Наличие библиотеки геометрических тел - от классических до менее симпатичных и экзотических форм - помогает как профессионалам, так и энтузиастам совершенствовать понимание структуры пространства. Модели таких твердых тел можно использовать в образовании, инженерии, архитектуре, а также в компьютерной графике и робототехнике.
Современные научные публикации и блоги служат источниками вдохновения и обмена информацией. В онлайн-пространстве можно найти подробные разборы исследований, ссылки на исходные коды проектов, а также активные дискуссии в социальных сетях, таких как BlueSky или Mastodon. Коммуникация с авторами и другими участниками стимулирует совместное развитие идей и способствует выявлению ошибок или пробелов в текущих теориях. Для тех, кто желает погрузиться в тему глубже, рекомендуется освоение навыков работы с современными компиляторами и языками программирования, такими как C++. Это позволит не только выполнять модификации существующих проектов, но и создавать собственные алгоритмы для поиска новых решений геометрических задач или обнаружения скрытых свойств устойчивых фигур.
Такие практики развивают критическое и аналитическое мышление, необходимые в научных исследованиях. Рупертова сфабрикованная куба и другие математические дыры служат ярким примером того, как кажущиеся на первый взгляд абстрактными математические объекты влияют на понимание пространства и формируют платформу для новых технологий и творческих задач. Их изучение расширяет границы человеческих знаний и стимулирует интерес к точным наукам среди различных возрастных групп и профессий. Таким образом, многогранники, начиная с классических форм и заканчивая необычными конструкциями вроде Рупертова сфабрикованного куба, представляют собой захватывающее поле для исследований, обучения и развлечений. Их свойства продолжают вдохновлять математиков, инженеров, педагогов и художников, открывая возможности для междисциплинарного взаимодействия и новых открытий в области визуализации, оптимизации и логического анализа.
Погружение в тайны многогранников позволяет по-новому взглянуть на привычный мир, осознать глубину и многообразие геометрии и открыть для себя невероятные математические "дыры", о которых ранее можно было лишь догадываться. .