Демонстрация алгоритмического квантового ускорения для абелевой задачи о скрытой подгруппе

Биткойн Скам и безопасность

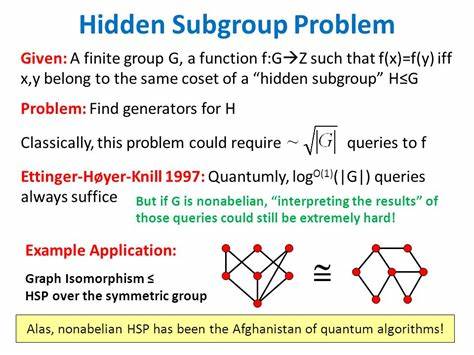
Квантовые вычисления в последние годы привлекают всё больше внимания как перспективное направление, способное радикально изменить подход к обработке информации и решению сложных задач. Одним из центральных вопросов этой области является достижение алгоритмического квантового преимущества — момента, когда квантовый компьютер решает определённую задачу существенно быстрее, чем классический. Недавние экспериментальные достижения принесли важный прорыв в июне 2025 года с публикацией исследования по демонстрации алгоритмического квантового ускорения для абелевой задачи о скрытой подгруппе. Задача о скрытой подгруппе (Hidden Subgroup Problem, HSP) занимает ключевое место в теории квантовых алгоритмов. В частности, её вариации лежат в основе многих известных квантовых алгоритмов, таких как алгоритм Шора для факторизации чисел и вычисления дискретного логарифма, а также алгоритм Саймона, открывший путь к доказыванию экспоненциального превосходства квантовых алгоритмов над классическими в модели оракулов.

Классическая формулировка задачи Саймона состоит в нахождении скрытого периода, кодируемого в 2-к-1 функции, где задача сводится к выявлению некоторого битового шаблона, повторяющегося в значениях. Идеальным решением является построение квантового алгоритма, который безошибочно и с экспоненциальной скоростью находит период, в то время как классические методы решают аналогичную задачу за экспоненциально большее время. Испытания и реализация подобных алгоритмов на реальном квантовом оборудовании ранее стояли на серьёзном пути из-за ограничений существующих квантовых процессоров — шумов, ошибок измерений и быстрого распада когерентности. Именно эти барьеры препятствовали демонстрации реального квантового преимущества на практике. В рамках нового исследования учёные использовали два квантовых процессора IBM Quantum, каждый из которых содержит 127 сверхпроводниковых кубитов.

Это оборудование считается одним из самых масштабных и современных доступных в индустрии. Для адаптации задачи и алгоритма к реальным условиям они выбрали вариант задачи Саймона c ограниченным весом Хэмминга спрятанного периода, что позволило эффективно уменьшить ресурсные требования. Благодаря применению методов динамического декуплинга — техники, позволяющей снизить влияние окружающего шума и продлить когерентность кубитов, а также методам коррекции ошибок измерений — исследователи смогли значительно улучшить качество вычислений. Эти методы вместе позволили проводить более надёжные и точные эксперименты на квантовом оборудовании. Экспериментальные данные подтвердили, что для значений веса Хэмминга достаточно малых величин и при использовании цепочек длиной до 58 кубитов достигается настоящая экспоненциальная скорость решения по сравнению с классическими алгоритмами.

Хотя качество ускорения оказалось ниже идеального предсказания для безошибочной модели, его наличие очевидно подтверждает квантовое преимущество в реальных условиях. Это прорывное достижение стало важным мостом между теоретической разработкой квантовых алгоритмов и их практической реализацией на шумных промежуточных квантовых устройствах (NISQ). Демонстрация алгоритмического квантового ускорения, впервые показанная для абелевой скрытой подгруппы, открывает новые горизонты для разработки сложных алгоритмов, применимых для криптографии, оптимизации, химических симуляций и других наукоёмких задач. Нестабильность и шумы квантовых процессоров изначально делают реализацию мощных квантовых алгоритмов крайне сложной, но с прогрессом методов подавления ошибок и расширением масштабов процессоров ситуация кардинально меняется. В частности, динамический декуплинг доказал свою эффективность не только в снижении однотипных шумов, но и в подавлении сложных кросстолков и коррелированных искажений, что особенно важно при работе с большим количеством кубитов.

Кроме того, в исследовании развивается направление исправления ошибок измерения — одна из ключевых проблем в квантовых вычислениях, где неточные результаты обычно искажают конечный вывод. Методология итеративного байесовского развёртывания, используемая в эксперименте, содействовала существенно повысить точность выходных данных, делая качество квантовых вычислений всё более сопоставимым с классическими стандартами. Сама по себе задача о скрытой подгруппе имеет фундаментальное значение, ведь многие важные квантовые алгоритмы можно свести к её решению. Таким образом, экспериментальный успех в решении этой задачи на реальных квантовых процессорах — это не просто ещё один показатель повышения производительности, но и заверение того, что квантовые машины становятся функционально пригодными для выполнения сложных вычислений, выходящих за рамки возможностей классической техники. Важность данной работы подчёркивается глобальными трендами в области развития квантовых технологий.

С каждым годом увеличивается количество кубитов в устройствах, улучшается качество логических операций и снижается уровень фонового шума. Растут инвестиции от научных организаций и корпораций, поддерживающих разработку квантовых платформ, что неминуемо ускоряет претворение в жизнь перспектив квантового превосходства. Перспективы дальнейших исследований включают расширение диапазона параметров задачи, увеличение числа кубитов и совершенствование методов коррекции ошибок и управления шумами. Такое объединение аппаратных и программных усовершенствований позволяет надеяться, что очень скоро появятся ещё более весомые демонстрации квантового преимущества, а также практические приложения на стыке информатики, физики и математики. Работа по демонстрации квантового ускорения для абелевой задачи о скрытой подгруппе — это важный этап на пути к построению универсальных квантовых компьютеров с реальным преимуществом.

Она показывает, что квантовые вычисления перестают быть чисто теоретической концепцией и становятся всё более применимой технологией с огромным потенциалом для будущего науки и индустрии. Таким образом, внедрение современных методов борьбы с шумами, прогресс в квантовом аппаратном обеспечении и выбор адаптированных задач позволяют уже сегодня получать экспоненциальные выигрыши в скорости. Это достижение укрепляет уверенность в том, что будущее за квантовыми технологиями, способными решать задачи, ранее считавшиеся невыполнимыми.