Загадка Сангаку: Почему радиус малого круга равен 4/33 стороны квадрата

Инвестиционная стратегия Стартапы и венчурный капитал

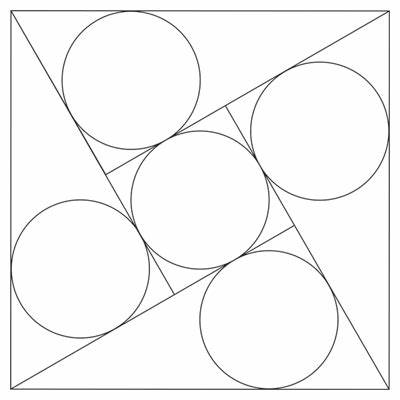
Сангаку представляет собой класс традиционных японских геометрических задач, которые были написаны на деревянных табличках и размещались в святилищах и храмах периода Эдо. Эти красивые и зачастую сложные задачи кружат вокруг кругов, треугольников и квадратов, создавая уникальные геометрические композиции, которые вдохновляют как любителей математики, так и художников. Недавно одной из таких загадок заинтересовалась группа энтузиастов, пытаясь найти радиус небольшого круга внутри квадрата с некоторыми вписанными окружностями. Результат получился интригующим - радиус этого маленького круга оказался равен 4/33 длины стороны квадрата. Почему именно так, и как к этому прийти? Давайте подробно рассмотрим задачу и методы решения.

Изначально задача кажется достаточно сложной из-за большого количества данных и геометрических ограничений. В квадрат вписаны три больших полуокружности, и между ними расположен маленький круг, касающийся всех трёх. Цель - найти радиус этого малого круга относительно длины стороны квадрата, обозначенной как s. Проблема осложняется необходимостью учитывать касательность и положение всех окружностей, что приводит к сложным системам уравнений. Одним из первых шагов является разумный выбор системы координат.

Например, можно расположить квадрат четко на координатной плоскости, закрепив левый нижний угол в начале координат (0,0), а сторону квадрата вдоль осей X и Y. Это позволяет задавать координаты центров больших полуокружностей и маленького круга в удобных выражениях. Центры трех больших полуокружностей можно обозначить как точки (0,s/2), (s/2,0) и (s,0) с радиусами s/2, s/2 и s соответственно. Для малого круга предлагается координаты центра (h,k) и радиус r. Поскольку круги касаются друг друга, существуют уравнения, устанавливающие расстояния между центрами равными сумме или разности радиусов.

 

В итоге формируется система из трех уравнений, связывающих h, k и r. Метод решения системы уравнений включает использование формул для расстояния между точками, возведение в квадрат обеих частей уравнений для устранения корней и последующее вычитание уравнений для нахождения связей между h, k и r. Вычитание позволяет избавляться от квадратичных членов и получать линейные зависимости, например выражать h через r, а затем k через r и h. Таким способом был найден интересный факт, что h = 3r, а k = 5r, что уже упрощает понимание расположения маленького круга в координатной плоскости. Подставляя найденные выражения обратно в одно из уравнений, можно вывести уникальное значение радиуса r через длину стороны квадрата s.

 

После необходимой алгебраической обработки получается соотношение r = (4/33)s. Этот ответ кажется неожиданным и несколько непривычным, поэтому вызывает желание найти более геометрически интуитивное понимание. Один из таких альтернативных путей решения - метод инверсии, который широко используется в решении задач Сангаку. Инверсия - это преобразование на плоскости, которое меняет окружности и линии местами при сохранении касательности. Применяя инверсию относительно точки соприкосновения больших окружностей, можно упростить сложный набор касаний в более простую конфигурацию с тремя взаимно перпендикулярными линиями и окружностью, касающейся этих линий.

 

Решить задачу в перевернутой системе легче, а затем, применив обратную инверсию, получить искомые параметры исходной задачи. Идея заключается в том, что под воздействием инверсии три большие полуокружности, которые касаются друг друга и ограничивают пространство малого круга, принимают вид трех прямых линий. Малый круг становится окружностью, касающейся этих линий. Геометрия упрощается и можно получить равенства для параметров окружности, после чего обратная инверсия возвращает значения в исходную систему координат. Кроме того, задачи такого рода часто решаются при помощи подходов, связанных с теоремой Декарта о четырех взаимно касающихся окружностях.

Эта теорема задает строгие алгебраические отношения между радиусами четырех окружностей, касающихся друг друга, что позволяет установить уравнение для искомого радиуса. В рассмотренной Сангаку именно этот подход помог найти чистое численное выражение радиуса. Помимо математической части, задача имеет эстетическое и образовательное значение. Создание витража на основе этой загадки позволило визуализировать сложную геометрию и подойти к ней творчески. Математическое искусство помогает раскрыть красоту абстрактных законов через форму и цвет, что особенно интересно для изучающих математику и преподавателей.

В заключение, загадка Сангаку с малым окружностью внутри квадрата с тремя большими полуокружностями является прекрасным примером, как традиционные задачи гармонично соединяют глубокую геометрию, современную аналитику и художественное оформление. Ответ радиуса r=4/33s не только демонстрирует изящество древних знаний, но и стимулирует изучение новых методов, таких как инверсия и теорема Декарта, в современной математике. Эта задача является мостом между эпохами и способна вдохновить множество следующих поколений исследователей и творцов. .