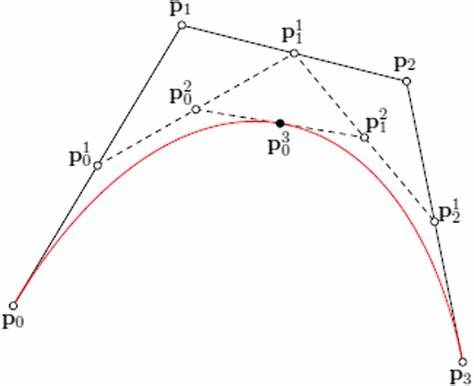
Кривые Безье — это один из фундаментальных инструментов, применяемых в области графики, дизайна и моделирования, позволяющий создавать гладкие, органичные линии и формы. Интерполяция кривой Безье предполагает процесс построения кривой, которая точно проходит через заданные опорные точки, обеспечивая высокий уровень контроля над ее формой и поведением. Эта особенность делает кривые Безье незаменимым инструментом для множества задач, включая проектирование шрифтов, анимацию, техническое черчение и визуализацию данных. Основы кривых Безье восходят к работам французского инженера Пьера Безье, который в 1960-х годах разработал эти параметры для использования в автомобильном дизайне. Главная идея заключается в том, что сложную кривую можно представить уравнением, определяемым несколькими контрольными точками.
От этих точек зависит весь характер изгиба — насколько он плавный, крутой или изменчивый. Классическая кривая Безье второго и третьего порядка широко используется в практике, поскольку позволяет подогнать форму под конкретные нужды. Интерполяция отличается от аппроксимации тем, что в первом случае кривая проходит точно через все заданные точки, а во втором — лишь стремится к ним, не гарантируя точного совпадения. Это делает интерполяцию особенно ценной при точных инженерных или дизайнерских расчетах, где важна каждая координата. Процесс создания интерполированной кривой Безье начинается с выбора набора заданных точек, которые кривая должна проходить.
Далее вычисляются специальные контрольные точки, расставленные таким образом, чтобы обеспечить непрерывность и гладкость линии. Для решения этой задачи используются различные математические методы, включая систему линейных уравнений, полиномиальную интерполяцию и сплайны. Особое внимание уделяется обеспечению непрерывности первого и второго порядка, что влечет за собой плавность переходов и отсутствие резких изломов. Значительную роль играет порядок кривой Безье. Чем выше порядок, тем больше контрольных точек используется и тем сложнее форма кривой.
Однако при увеличении порядка повышается и вычислительная сложность, а также возрастает риск возникновения артефактов и нелогичных изгибов между точки. Поэтому часто прибегают к разделению задачи на несколько сегментов, объединенных в составную кривую, чтобы сохранить удобство управления и поддерживать высокое качество результата. Технологии построения интерполирующих кривых Безье особенно актуальны в цифровой графике и анимации, где требуется создавать плавные и предсказуемые движения или формы. В программных продуктах для векторного рисования и автоматизированного проектирования (CAD) данный подход применяется для повышения точности и красоты изображений, позволяя воссоздать реальные объекты с высоким уровнем детализации. Важным аспектом работы с кривыми Безье является управление их параметризацией.
Неравномерное распределение параметров вдоль кривой влияет на ее форму, способствуя большей или меньшей натяженности между точками. За счет настройки этих значений можно добиться оптимального баланса между точностью интерполяции и плавностью линии. Современные алгоритмы предлагают способы автоматического подбора параметров, облегчая задачу и минимизируя влияние человеческого фактора. Помимо технической стороны, интерполяция кривых Безье тесно связана с художественным видением. Гибкость этого инструмента позволяет дизайнерам оценивать и модифицировать форму, добиваясь уникального визуального стиля и функциональности.
Возможности корректировать кривую практически в реальном времени делают данный процесс интерактивным и творческим. Следует отметить, что наряду с историческими и классическими методами сегодня активно разрабатываются новые техники, интегрирующие машинное обучение и оптимизационные алгоритмы. Они позволяют улучшить качество интерполяции, особенно в условиях больших объемов данных или сложных форм, обеспечивая высокую точность и экономию ресурсов. Для практикующих специалистов полезным будет использование специализированных программных библиотек, реализующих вычисления кривых Безье и их интерполяцию. Среди популярных решений — библиотеки на Python, C++, JavaScript, которые облегчают задачу построения, визуализации и интеграции кривых в проекты.
В итоге, изучение и применение интерполяции кривых Безье раскрывает широкие возможности для создания качественных, точных и эстетичных графических объектов. Благодаря сочетанию математической строгости и гибкости визуального дизайна, данная технология сохраняет высокую актуальность и востребованность в самых разных областях. Мастерство владения принципами интерполирования помогает создавать проекты, отражающие как технические требования, так и художественную утонченность.