Современные технологии стремительно развиваются, и методы обработки больших данных становятся все сложнее и многограннее. Одним из таких подходов, получивших значительное внимание в последние годы, является использование графовых векторных индексов. Чтобы понять их суть, полезно обратиться к теореме FES — фундаментальному принципу, раскрывающему основы их функционирования. В данной статье рассматривается, что собой представляют графовые векторные индексы, как теорема FES позволяет объяснить ключевые механизмы их работы, а также почему эти методы считаются одними из самых мощных для поиска и организации данных в различных сферах информационных технологий. В первую очередь, стоит отметить, что векторные индексы широко применяются для обработки данных, представленных в виде векторов признаков.
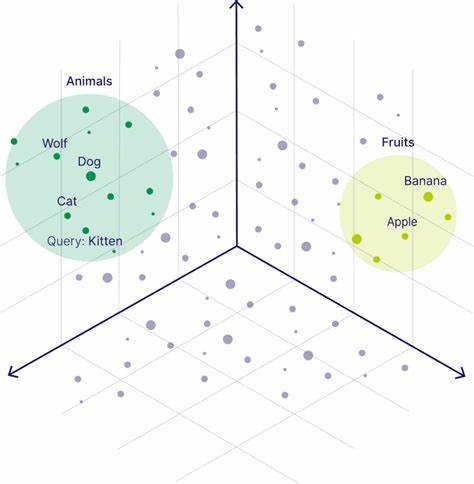
Такие данные характерны для задач машинного обучения, компьютерного зрения, обработки естественного языка и других областей. Однако с ростом объема и сложности информации традиционные методы индексирования становятся неэффективными, особенно при высоких размерностях пространства. Именно здесь на помощь приходят графовые векторные индексы, объединяющие графовые структуры и методы векторного поиска для оптимизации скорости и качества результата. Основная идея графовых индексов заключается в представлении векторных данных как вершин графа, где рёбра отражают близость или сходство между векторами. Это позволяет алгоритмам поиска использовать структуру графа для быстрого перехода между близкими по признакам точками, тем самым минимизируя количество рассчитываемых расстояний и ускоряя получение релевантной информации.
Теорема FES, кратко говоря, описывает два ключевых свойства таких графов: First property — эффективность локального поиска, обеспечивающая возможность быстрого приближения к целевому вектору с помощью постепенного перехода по ближайшим соседям; Second — стабильность структуры графа в условиях динамического добавления или удаления элементов без значительной потери производительности; и Third — гарантии обеспечения полного покрытия пространства данных, чтобы не упустить важные соседства при поиске. Несмотря на математическую сложность теоремы, её применение позволяет строить алгоритмы, гарантированно обеспечивающие баланс между скоростью и точностью при работе с большими векторными наборами. Преимущества графовых векторных индексов очевидны: высокая скорость поиска, снижение вычислительной нагрузки, адаптивность к динамическим изменениям данных и улучшенная масштабируемость. Особенно ценным этот подход становится в системах рекомендательных сервисов, поисковых движках, системах распознавания образов и в аналитике больших данных. Примером внедрения графовых индексов служат такие технологии, как Hierarchical Navigable Small World (HNSW) и Annoy, широко используемые для приближенного поиска ближайших соседей.