В современном мире программирование становится не только инструментом создания сайтов или приложений, но и мощным средством для решения даже таких увлекательных физических задач, как сборка сложных деревянных головоломок. Опираясь на точность и безукоризненную логику компьютера, можно существенно облегчить поиск решения, который человеку при всех усилиях подчас дается с трудом. Зачастую, особенно в случае головоломок, построенных из множества взаимосвязанных частей, поисковая область решений становится слишком большой для человеческого мозга. Именно здесь функциональный язык Haskell позволяет тщательно и эффективно смоделировать задачу и найти ответ с помощью глубокого системного подхода. Недавно был представлен интересный проект, в основе которого лежит решение трехмерной головоломки с помощью Haskell.
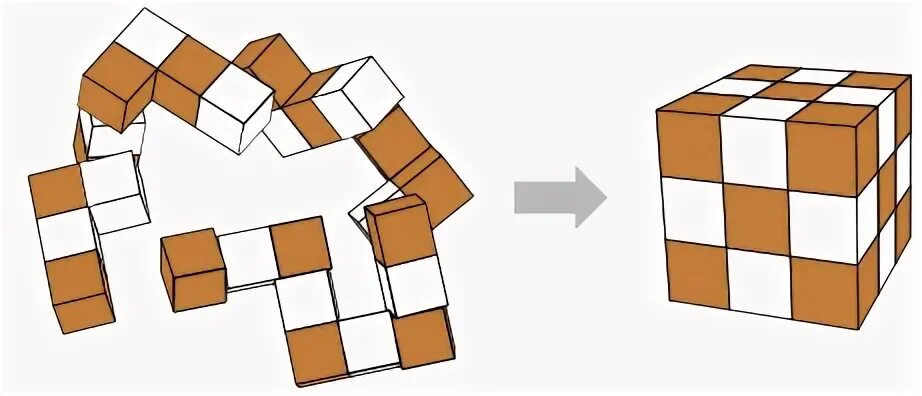
Суть головоломки состоит в том, чтобы собрать пятнадцать одинаковых деревянных элементов в трехмерный куб размерами 5х5х5 единиц. Каждый отдельный элемент представляет собой "ствол", размером 4х1х1 единиц с выступающей квадратной выемкой размером 1х1х1, которая при сборке головоломки играет ключевую роль. Задача - плотно упаковать все части в куб без пустот и выступающих за рамки элементов. Такая задача требует не просто пространственного воображения, но и математической точности, поскольку дискретный характер кубов и простая геометрия открывают потенциал для программного перебора вариантов. В основе моделирования лежит принцип декомпозиции пространства на элементы - ваноксы - единичные кубики с целочисленными координатами в трехмерном пространстве.
Каждая точка в пространстве задается вектором из трех целых чисел, что позволяет идеально описать положение каждой составляющей головоломки. Для работы с трехмерной геометрией используется тип V3 Int из специализированной библиотеки линейной алгебры, что повышает удобство и читабельность кода. Данные подходы создают структуру, позволяющую приступить к реализации решения. Описание отдельного элемента головоломки производится через набор векторов, координатирующих кубики, из которых он состоит. Оргинальный элемент позиционируется так, что основной "ствол" тянется вдоль координаты z от 0 до 3, а выступающий элемент расположен в точке (0, 1, 2).
Используя этот "шаблон" элемента, все остальные экземпляры головоломки могут быть получены за счет поворотов и перестановок. Такая концепция упрощает последующий перебор вариантов и задает основу для алгоритмического решения. Движение элемента в пространстве описывается через две трансформации: матрицу вращения размером 3×3, задающую ориентацию детали, и вектор трансляции, определяющий положение в пространстве. Хранение этих данных осуществляется в специальной структуре Disposition, где сохранены матрица и вектор в числовом формате. Благодаря таким подходам появляется возможность работать с каждым элементом головоломки уже не как с абстрактной фигурой, а в виде математически строгого объекта с координатами.
Применение вращения и смещения к базовой модели элемента позволяет получить полный набор координат всех кубиков в конкретном расположении, что важно для проверки валидности размещения. Важно отметить, что сначала применяется матричное вращение, а затем происходит смещение - это логическое следование этапам трансформации. Такая последовательность помогает сохранить интуитивную структуру решения и избежать ошибок. Благодаря этим преобразованиям можно приступить к созданию набора всех возможных расположений. Основной вызов при переборе дискретных трансформаций состоит в том, что множество потенциальных трансформирующих матриц и векторов бесконечно.
Для реализации решения возникла идея ограничить пространство поиска за счет оценки критериев валидности и формирования конечного списка кандидатов. Сужение множества вращений реализовано путем перебора всех матриц с коэффициентами из наборов -1, 0 и 1. Этот подход основан на том, что в головоломках с дискретной геометрией поворот оси либо оставляет ее неизменной, либо меняет местами с другой, инвертирует или переориентирует. Последовательный перебор всех таких матриц покрывает все возможные вращения, хотя и содержит некоторые невалидные варианты. Кандидаты на смещения выбираются из ограниченного диапазона целых координат от 1 до 5 включительно, что соответствует ограниченному пространству коробки головоломки.
Поскольку базовая точка элемента находится в начале координат, то при смещении в указанный диапазон гарантировано, что минимум один кубик не выйдет за пределы пространства, а остальные проверяются дополнительно. Такой выбор ограничивает поисковое пространство, делая задачу вычислительно реализуемой. Следующий важный этап - фильтрация тех кандидатов, которые не отражают корректные вращения. Ротация в трехмерии характеризуется матрицей, которая должна быть ортогональной и иметь определитель равный единице. Проверка таких условий отсекает неподходящие трансформации, исключая зеркальные отражения, масштабирования и другие искажения, которые не подходят для описания физического поворота кубика.
Такая проверка реализуется через умножение матрицы на её транспонированное отображение и вычисление определителя. Ещё одним обязательным условием корректного расположения является полное попадание всех частей детали в рамки коробки размером 5х5х5. Проверка заключается в пролистывании всех кубиков трансформированного элемента и подтверждении, что все их координаты удовлетворяют заданным граничным условиям. Этот дополнительный фильтр гарантирует, что элементы не выходят за пределы игрового пространства, а значит, подходят для потенциального включения в финальное решение. После комплексной фильтрации кандидатов получается конечный и полный набор валидных размещений элемента головоломки.
Такое преобразование из бесконечного пространства в конечный набор существенно упрощает задачу поиска, повышая эффективность дальнейших вычислений и минимизируя избыточные проверки. Заключительный этап первого этапа решения - превращение списка валидных расположений в массив трехмерных координат кубиков. Это необходимо для дальнейшего построения алгоритма поиска, который будет работать с набором конкретных точек, а не с абстрактными трансформациями. Именно с этим набором конкретных координат можно приступить к сборке, перебору и поиску комбинаций, подходящих для полного куба без разрывов. Используя силу Haskell, функциональный язык, известный своей лаконичностью и мощью для математического и логического моделирования, можно организовать решение, которое четко и корректно работает с пространственными структурами и трансформациями.
Haskell позволяет определить строгие типы для всех элементов и операций, что снижает вероятность ошибок и облегчает поддерживаемость кода. Помимо этого, благодаря декларативной природе языка, код становится легче для восприятия при анализе сложных алгоритмов. Первая часть данного подхода служит фундаментом, заложенным в осмысленном понимании самой структуры задачи. Создание корректной модели пространства и элементов, грамотное определение множества трансформаций и реализация проверки валидности предоставляет основу безопасности и эффективности последующих шагов. Вторая часть решения уже запускает механизм поиска и оптимизации, позволяя получить ответ на сложную задачу головоломки.
Итогом становится пример того, как с помощью современных средств программирования и математического аппарата можно применять вычислительные методы для решения физических задач, выходящих за рамки традиционного прямого поиска. Это наглядный пример симбиоза инженерного мышления и алгоритмической точности, где человеческая логика формируется в понятные машине инструкции, что приводит к успешному исполнению непростой задачи. Представленная методология может быть успешно адаптирована и для других пространственных задач с дискретной структурой, будь то трехмерное моделирование, проектирование или игры. Ее потенциал выходит далеко за рамки одной головоломки, открывая дорогу к новым подходам в исследовании объемных структур и поиска оптимальных решений в ограниченных пространствах. .