Музыкальные лады – фундаментальный элемент в теории и практике музыки, определяющий структуру и характер звучания мелодий и гармоний. В основе лада лежит последовательность интервалов, которые создают уникальный музыкальный контекст вокруг выбранного тона — корня. Чтобы глубже понять природу ладов и их генерацию, полезно рассмотреть их с математической и алгоритмической точек зрения. Одним из интересных подходов к описанию ладов является представление их как мультиперестановок из элементов 0 и 1, расположенных в двенадцати местах — по числу полутонов в октаве. Такой подход не только расширяет возможности генерации всех возможных ладов, но и предлагает новый взгляд на структуру музыкальных формул.
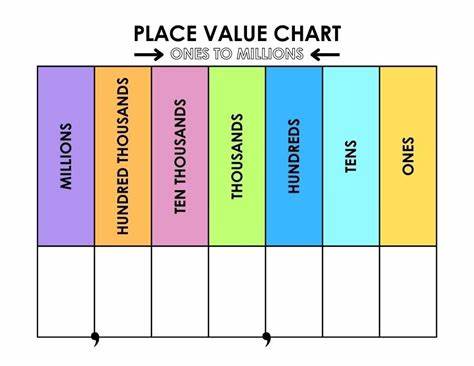
В музыкальной теории лад часто задаётся через набор нот, соотносящихся с корнем по определённым интервалам — по количеству полутонов от корня. Например, мажорный лад на ноте до (C) включает ноты до, ре, ми, фа, соль, ля, си, что можно выразить интервалами 0, 2, 4, 5, 7, 9 и 11 полутона от тоники. Такой лад можно описать серией шагов, например, последовательностью интервалов между соседними нотами: целый шаг, целый шаг, полутона, целый шаг, целый шаг, целый шаг и полутона (WWHWWWH). Но для генерации произвольных ладов удобнее работать именно с интервалами от всякой ноты к корню, чтобы создавать наборы, которые отражают все возможные варианты звуковой структуры. Идея использования списка из 12 элементов, наполненного 0 и 1, вытекает из принципа разбиения октавы на части длиной по одному полутона.
Элементы 1 и 0 в такой последовательности обозначают, соответственно, начало новой ноты и продолжение предыдущей или отсутствие изменяющегося интервала. Куски последовательных одинаковых элементов могут интерпретироваться как интервалы между нотами, а длина каждого кусочка — как величина интервала. Примером может служить строка из двоичных символов «001101100110», где последовательности 0 и 1 вместе формируют структуру мажорного лада. Такой подход позволяет представить лад как мультиперестановку, то есть перестановку с повторениями, которые в данном случае ограничены элементами 0 и 1. Использование мультиперестановок базируется на том, что все двоичные вариации длиной 12 будут учитывать каждый возможный вариант разбиения октавы, а количество этих вариаций равно 2 в степени 12, то есть 4096.
Ключевым этапом является преобразование подобной двоичной последовательности в формулу, где каждая последовательность однородных цифр — это количество полутонов интервала между соседними нотами. Такая формула выступает как основа для записи лада в формате последовательности интервалов. Далее, путём накопления суммы этих интервалов можно получить список интервалов каждой ноты относительно корня, который и определяет конкретный лад. В результате получается полный набор из всех возможных формул ладов, которые можно использовать для теоретического анализа или композиторских экспериментов. Это открывает грандиозные возможности для автоматизированного создания новых масштабов и звучаний, выходящих за рамки традиционных мажорных и минорных ладов, включая экзотические варианты и даже не диатонические структуры.
Практическое применение такого алгоритмического подхода находит отражение в программном обеспечении для генерации и анализа музыкальных масштабов. С помощью функционального программирования, в частности языка Elixir, можно создать функцию, которая перебирает все мультиперестановки, преобразует их в интервальные формулы и применяет для построения ладов с различными корнями и написаниями нот (spelling), что позволяет создавать разнообразные музыкальные инструменты и обучающие программы. Помимо генерации, важной составляющей является тестирование корректности полученных ладов. Для этого можно использовать property-based testing, проверяя, что длина созданного лада совпадает с длиной формулы, а также что интервалы между нотами соответствуют заявленным. Такой системный подход обеспечивает надёжность и точность генератора, что критично для использования в музыкальной теории и практике.
Хотя данный метод даёт исчерпывающий набор формул масштабов, всегда стоит задаваться вопросом, насколько все эти варианты осмысленны с музыкальной точки зрения. В этом плане возможны более элегантные и семантически насыщенные подходы, которые учитывают не только чистую математику, но и эстетические, функциональные особенности ладов в разных музыкальных традициях и стилях. Например, работа с классическими модальными системами, микроинтервалами и экспериментальными звуковыми паттернами может потребовать иных математических моделей и предложить иные способы генерации. Тем не менее, рассмотрение ладов как мультиперестановок из 0 и 1 в двенадцати позициях остаётся мощным инструментом для исследователей музыки и разработчиков программного обеспечения. Он помогает визуализировать полноту пространства возможных масштабных формул и служит основой для дальнейших открытий в мире музыкальной математики.
В итоге, объединяя музыкальную теорию с алгоритмами и функциональным программированием, можно создавать инновационные решения для создания, изучения и освоения музыки, что будет полезно как композиторам, так и преподавателям, а также всем, кто интересуется глубинами звука и гармонии.