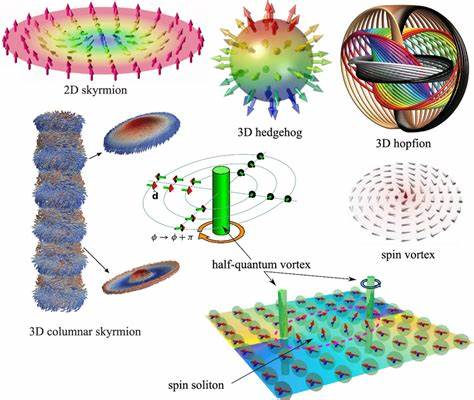
Аморфные тела, такие как стекла и полимеры, обладают сложной и неупорядоченной структурой, которая на первый взгляд затрудняет применение классических понятий о дефектах, известных из науки о кристаллах. Однако понимание микроскопических механизмов пластической деформации в таких материалах критически важно для развития современных технологий и создания материалов с заданными свойствами прочности и гибкости. В последние годы учёные всё активнее используют топологические методы для описания дефектов, которые играют ключевую роль в механической деструкции аморфных твёрдых тел. В частности, концепция ежевидных топологических дефектов (hedgehog topological defects, HTD) приобрела особое значение для описания пластики в трёхмерных системах. Традиционно понятие топологических дефектов развивалось на примере кристаллических материалов, где наличие упорядоченной структуры позволяет чётко определить дислокации и дисклокации как носители пластической деформации.
В аморфных системах отсутствует дальний порядок и даже квазидальний порядок, что мешает однозначно идентифицировать дефекты подобного рода. Тем не менее, последние исследования показывают, что можно переосмыслить понятие дефектов в контексте аморфных сред, опираясь на векторные поля, описывающие колебания или деформации в материале. Ежевидный топологический дефект — это точечный дефект, характеризуемый векторным полем, в котором направления векторов расходятся или сходятся подобно иголкам ежа. Для трёхмерных аморфных тел такой дефект описывается интегралом, дающим топологический заряд Q, который формально является инвариантом при гладких деформациях поля. Однако в отличие от двумерных систем, где знак дефекта напрямую указывает на его физическую суть, в трёхмерных аморфных телах знак Q оказывается неоднозначным из-за свойств векторного поля — оно может быть инвариантно относительно инверсии направления векторов.
Основное отличие и новизна подхода к ежевидным дефектам в 3D аморфных телах заключается в выделении не только топологических характеристик, но также геометрических свойств дефектов. Ключевым параметром оказывается геометрия расходимости или сходящести векторов вокруг дефекта: они могут формировать либо радиальную конфигурацию с равномерным расходящимся векторным полем, либо гиперболическую конфигурацию с выраженными седловыми характеристиками. Именно гиперболическая геометрия ассоциируется с дефектами, тесно связанными с зонами повышенной пластической активности, так называемыми «мягкими точками» (soft spots). Важная часть исследований проводилась с помощью компьютерных симуляций полимерного стекла, реализованного в модели Креймера–Греста. Использовалась концепция анализа спектроданных Гермического матрицы сил, где вычислялись собственные значения и собственные векторы, описывающие нормальные моды колебаний системы.
Ежевидные дефекты выявлялись в поле собственных векторов, а также в полях смещений, возникающих при деформации. Такие подходы позволяют выявить локализации пластических событий ещё до их фактического возникновения, что является мощным инструментом для предсказания разрушения материала. Наблюдения показывают, что распределение ежевидных топологических дефектов по частотам колебаний следует законам, сходным с распределением плотности состояний в стеклах, что указывает на глубокую связь между динамическими свойствами и топологическими объектами. Кроме того, выявлена тенденция к кластеризации дефектов с разноименными зарядами, свидетельствующая о стремлении системы свести суммарный топологический заряд к минимуму, подобно парообразованию вихрей и антивихрей в двумерной физике жидкости. Особо примечательно, что в трёхмерных аморфных системах корреляция между дефектами и зонами пластической активности не зависит от знака топологического заряда, в отличие от двумерных аналогов, где отрицательно заряженные дефекты играют более значимую роль.
Здесь геометрия дефектов, а именно гиперболический характер поля, выступает более релевантным индикатором мест предрасположенности к пластическим преобразованиям. Дальнейшие исследования фокусировались на анализе неаффинных полей смещений, возникающих при атермальном квазистатическом сдвиге в системе. Результаты показывают, что ежевидные дефекты в данных полях имеют ещё более тесную связь с пластическими «мягкими точками» и динамическими событиями деформации. Это очень значимо с практической точки зрения, так как в экспериментальных условиях наблюдать именно методы спектрального анализа затруднительно, а поля смещений доступны для измерения в современных экспериментальных установках, например, в студиях коллоидных стекол или гранулированных систем. Кроме того, доказано, что тип геометрии дефекта влияет на его устойчивость и склонность инициировать пластическую деформацию.
Гиперболические дефекты проявляют более выраженные «седловые» характеристики и могут истолковываться как локальные регионы с повышенной неустойчивостью, благоприятные для структурных перестроек. Это согласуется с идеями о том, что пластические события в аморфных твердых телах не являются случайными, а обусловлены локализованными зонами, обладающими специфической структурой и динамикой. Результаты исследовательской работы имеют важные последствия для теоретического понимания пластических процессов в аморфных материалах, а также для разработки новых методов прогнозирования хрупкости, предпосылок для разрушения и механических качеств веществ. Идентификация и классификация ежевидных топологических дефектов могут стать основой для создания универсальной теории пластичности в трёхмерных аморфных системах, аналогичной той, что существует для кристаллов. Практическая реализация алгоритмов для обнаружения и анализа ежевидных дефектов в экспериментах также становится предметом активного развития.
Предложенные методы могут быть применены к данным, полученным в экспериментах над гранулами, коллоидными частицами и другими моделями аморфных систем, что позволит проверить теоретические предсказания и расширить понимание природы пластической деформации. Итогом работы является подтверждение того, что топологический и геометрический анализ векторных полей в аморфных твёрдых телах предлагает новый, мощный инструмент для выявления истоков пластической деформации на микроскопическом уровне. Особое внимание уделяется гиперболическим ежевидным дефектам, роль которых неоспорима в процессах зарождения и развития пластических событий. Дальнейшее развитие этих идей обещает принести значимые результаты в области материаловедения и физики твёрдого тела. В частности, понимание взаимодействия между топологическими объектами и геометрическими особенностями структуры может позволить управлять механическими свойствами материалов на этапе их проектирования, открывая перспективы для создания новых высокопрочных и при этом пластичных аморфных материалов.
Таким образом, ежевидные топологические дефекты в трёхмерных аморфных телах представляют собой ключ к раскрытию механизма пластичности, соединяя в себе глубокие математические концепции и экспериментальные наблюдения. Эти открытия расширяют горизонты фундаментальной физики и практически важны для инженерных приложений, делая перспективным дальнейшее изучение топологической природы дефектов в сложных неупорядоченных системах.