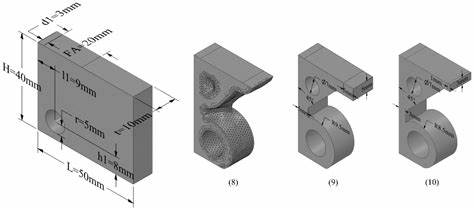
Современные задачи проектирования инженерных конструкций требуют не только высокой точности, но и способности эффективно адаптироваться под различные условия эксплуатации. Параметрическая оптимизация форм становится одним из ключевых инструментов в области компьютерного моделирования и дизайна, позволяя максимально эффективно использовать материалы и создавать конструкции с оптимальными эксплуатационными характеристиками. Одним из наиболее мощных подходов для решения таких задач служит дифференцируемый метод конечных элементов (FEM), который благодаря интеграции с системами автоматического дифференцирования позволяет проводить градиентный спуск непосредственно по параметрам формы. Такой подход открывает новые горизонты для разработки сложных инженерных систем и материалов. Параметризация форм сводится к выбору набора переменных, которые задают геометрию конструкции.
В рассматриваемом случае структура моделируется как совокупность стержней или балок, каждый из которых представлен набором сегментов с определёнными координатами вершин. Задача сводится к тому, чтобы изменить положение этих вершин, например, по оси Y, таким образом, чтобы добиться минимальной деформации или повышения жёсткости конструкции при заданных нагрузках. Вместо классического топологического подхода, где оптимизация ведётся по плотности материалов в каждой точке сетки, применяется параметрический метод, который работает с дизайнерскими переменными на уровне элементов структуры. Дифференцируемость в таком контексте чрезвычайно важна, так как позволяет использовать современные методы градиентного оптимизационного поиска. Однако, ряд операций, связанных с обработкой геометрии, например вычисление поля подписанного расстояния (signed distance field, SDF) с помощью библиотек, не поддерживающих автоматическое дифференцирование, представляют собой вызов.
Для обхода этого ограничения применяется численная аппроксимация якобиана из технологии конечных разностей. Таким образом, весь конвейер – от параметров формы, через вычисление поля подписанного расстояния, формирование плотности материалов до решения краевой задачи методом конечных элементов – становится дифференцируемым. Ключевым компонентом такой системы является библиотека Tesseract, которая позволяет модульно оборачивать необходимые вычисления в отдельные, взаимосвязанные узлы (называемые тессерактами). Каждый из этих модулей реализует не только прямое вычисление функций, но и соответствующие дифференцируемые интерфейсы, такие как вычисление векторно-якобианового произведения. Это даёт крайне мощный и масштабируемый инструмент, позволяющий строить сложные вычислительные пайплайны без необходимости монолитной реализации и облегчает поддержку и расширение кода.
Что же касается реализации самого вычисления геометрии, то в качестве основы применяется библиотека PyVista, которая формирует 3D-модель конструкции из набора параметров, задающих стержни. Далее с помощью этой модели вычисляется поле подписанного расстояния – числовое поле, указывающее, насколько точка в пространстве удалена внутри или вне формы. Такое поле особенно удобно для применения в контексте оптимизации, так как позволяет изящно описывать границы материалов. Для обеспечения дифференцируемости этого этапа, несмотря на отсутствие непосредственной поддержки автоматического дифференцирования в PyVista, применяется метод конечных разностей с малыми шагами. Далее происходит преобразование поля подписанного расстояния в поле плотности материала, которое затем подается в FEM-солвер.
Преобразование осуществляет гладкую, дифференцируемую функцию на основе параметризованной сигмоиды, которая выравнивает переход между материалом и пустотой, контролируя её резкость и положение с помощью специальных параметров. Это гарантирует плавность функции плотности, что крайне важно для корректной работы градиентных методов оптимизации. Сам FEM-солвер реализован в библиотеке jax-fem и интегрирован в подсистему Tesseract, что обеспечивает поддержку полного автоматического дифференцирования. При этом в рамках вычислений жёстко заданы граничные условия, например закрепление всей левой части конструкции и приложение нагрузки справа внизу, что имитирует реальные инженерные задачи. Результатом работы FEM-солвера является вычисленная комплаенс – мера деформируемости конструкции, которую необходимо минимизировать для повышения жесткости.
Оптимизационный цикл базируется на градиентных методах с использованием библиотеки optax. Исходные параметры, задающие положение вершин стержней, обновляются так, чтобы минимизировать комплаенс. Расчёт градиентов производится сквозь весь «конвейер» – от параметров формы через вычисление SDF и плотности до результатов FEM. Такая цепочка дифференцируемых функций позволяет эффективно и быстро находить локальные минимумы целевой функции, улучшая конструкцию. В процессе работы наблюдается стабильное и резкое снижение комплаенса, что свидетельствует о корректной настройке и эффектиности работы всего пайплайна.
Параметры, отвечающие за смещения по оси Y, изменяются соответствующим образом, отражая адаптацию формы для повышения жёсткости и устойчивости. Визуализация промежуточных и конечных состояний формы показывает, как конструкция меняется от первичного расположения к оптимальному. Дополнительно при помощи анимации можно проследить эволюцию распределения плотности по ходу итераций, что является удобным аналитическим инструментом. Интересен факт, что предложенный параметрический подход показывает результаты, сопоставимые с классическим свободноформенным топологическим оптимизационным решением. При этом он существенно выигрывает с точки зрения управляемости формы, ее удобства для промышленного проектирования и возможности поддерживать производительные и воспроизводимые параметры инженерного продукта.
Такие достоинства делают этот метод оптимальным выбором для задач инженерного проектирования и исследовательских разработок. Завершение работы с Tesseract-тессерактами осуществляется корректным освобождением ресурсов, что также является частью устойчивого и грамотно спроектированного программного процесса. Благодаря модульной структуре, весь проект легко расширяется, подстраивается под более сложные схемы нагрузки, увеличивается либо уточняется уровень детализации модели, а также интегрируется в более крупные системы автоматизированного проектирования. Параметрическая оптимизация с дифференцируемым FEM-солвером представляет собой современный и эффективный подход, который совместил удобство параметрического управления геометрией с мощью численных методов физического моделирования и современного машинного обучения в области автоматического дифференцирования. Это открывает двери для создания инновационных конструктивных решений – от легких и прочных деталей для аэрокосмической индустрии до оптимизированных архитектурных форм с минимальным расходом материалов.
Внедрение таких технологий в промышленную практику позволит не только повысить качество продукции и её эксплуатационные характеристики, но и сэкономить ресурсы за счёт более рационального использования материалов. Кроме того, доступность и модульность современных инструментов вроде Tesseract и JAX-FEM делают данные методы приоритетными для дальнейших исследований и внедрения в области компьютерного инжиниринга и цифрового проектирования.