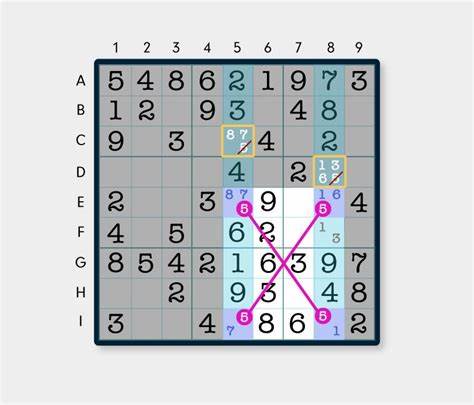
Судоку давно стало популярной головоломкой, покоряющей умы миллионов поклонников по всему миру. Задача решается путем разгадки числовой сетки 9 на 9 клеток, где необходимо так разместить цифры от 1 до 9, чтобы каждая цифра присутствовала ровно один раз в каждой строке, столбце и каждом из 3х3 блоков. Хотя сам процесс кажется простым для человека, программное решение требует тщательной разработки алгоритмов, обеспечивающих быструю и эффективную обработку всех возможных комбинаций. Одним из наиболее мощных способов решения судоку является метод Dancing Links (DLX), который решает задачу точного покрытия. Его разработка и совершенствование на современном языке Zig представляет собой интересное направление для оптимизации вычислений и углубленного анализа.
Алгоритм Dancing Links кардинально отличается от традиционных переборов. Он преобразует задачу решателя судоку в задачу точного покрытия, представляя все возможные решения как строки матрицы с бинарными значениями, где каждая строка удовлетворяет определённым ограничениям, а столбцы отражают сами эти ограничения. Задача сводится к выбору набора строк, при котором каждая колонка матрицы покрывается ровно одним значением 1. Это позволяет существенно сократить пространство поиска и ускорить процесс решения по сравнению с классическими методами. При моделировании судоку через точное покрытие создаётся матрица с 324 столбцами, разбитыми по четырём типам ограничений: каждая цифра должна присутствовать ровно один раз в каждой строке, каждом столбце, каждом 3x3 блоке и в каждой конкретной клетке.
При этом количество строк достигает 729 – это все возможные варианты размещения цифр в ячейках. Важно понимать, что для стандартной головоломки 9х9 такая матрица является разреженной, с относительно небольшим числом единичных элементов, что позволяет использовать структуру данных с указателями на соседние значения по четырём направлениям, не выделяя память под всю матрицу целиком. Такая реализация способствует быстрому обходу и обновлению матрицы в процессе рекурсивного поиска решения. Первые шаги алгоритма лежат в инициализации структуры данных, соответствующей исходной головоломке: все числа, уже известные в клетках, исключают альтернативные варианты для связанных по ограничению строк. После этого алгоритм начинается с выбора столбца, имеющего минимальное количество строк с единичными значениями – что помогает сократить время за счёт жадного выбора наименее численного ограничения.
Каждый выбранный вариант далее приводит к исключению противоречащих строк, что реализуется быстрыми операциями удаления ссылок благодаря механизму Dancing Links. Язык программирования Zig, известный своей эффективной работой с системными ресурсами и управлением памятью, позволяет создавать высокопроизводительные реализации, совмещающие низкоуровневую скорость с выразительностью кода. Разработка Sudoku-солвера с использованием DLX на Zig показывает, насколько важна оптимизация распределения памяти. Первоначально выделение памяти для каждой ячейки по отдельности приводило к большому количеству небольших операций, что негативно сказывалось на производительности. Однако переход к пакетной аллокации – выделение сразу всех четырёх связанных ячеек одной строки или даже всех ячеек сразу – позволил сократить количество операций выделения памяти в десятки раз.
Благодаря этому время решения одной головоломки снизилось с миллисекунд к их долям, что существенно увеличило пропускную способность приложения. Помимо оптимизации распределения памяти, важным этапом стала борьба с рекурсией. Хотя рекурсивный вызов является естественным для поиска в глубину в DLX, попытка полностью отказаться от него не привела к улучшению скорости из-за сложности управления стэком вызовов и состояния решения. Тем не менее внедрение компиляционных констант позволило оптимизировать вычисления, например, убрав затратный модульный оператор там, где длина линий известна на этапе компиляции. Такой подход лучше раскрывает возможности оптимизирующего компилятора и позволяет быстрее выполнять вычисления в критических местах кода.
Главное ускорение достиглось при переходе на режим компиляции ReleaseFast с включёнными оптимизациями на Zig. В этом режиме обработка головоломки занимает десятую долю миллисекунды, что является впечатляющим результатом для одного потока. Однако и многопоточная обработка задач позволила значительно увеличить производительность системы – распараллеливание решения сотен тысяч головоломок при помощи 20 потоков и правильного распределения задач достигло скорости более 130 тысяч судоку в секунду, а это порядка полумиллиарда головоломок в час. Важным акцентом при реализации стала трансформация DLX-структуры в «неуправляемую» версию, в которой память предоставляется извне. Такой подход избавляет от необходимости использования кучи и позволяет использовать только стек памяти, что существенно упрощает управление ресурсами и повышает работу кода под системными нагрузками.
Оптимизация подготовки данных до начала решения также сыграла значительную роль. Вместо того чтобы создавать полный набор ячеек и затем отсеивать неподходящие, теперь алгоритм пропускает создание линий для уже закрытых столбцов, что сокращает объём предварительных вычислений. Всё это в совокупности дало шанс добиться невероятной экономии времени, что в целом демонстрирует потенциал языка Zig для системных задач требовательных к высокой производительности и низкому потреблению ресурсов. Сравнение с реализациями на других языках, например, на Python или Swift, показывает, насколько критично правильно оптимизировать распределение памяти и работа с данными в подобных задачах. При этом сам DLX как метод позволяет решать не только судоку, но может быть адаптирован для решения задач N-ферзей и других точных покрытий.
Результаты демонстрируют, что даже при простом коде с умелым подходом к архитектуре данных и ресурсам можно добиться значительных приростов в скорости – что важно при создании высокопроизводительных алгоритмических сервисов. Помимо практической пользы, данный опыт развития и оптимизации DLX на Zig служит прекрасной демонстрацией принципов эффективной программной инженерии – понимания структуры данных, контроля памяти, профилирования производительности и балансирования между удобством и скоростью. Использование современных средств для измерения, таких как Hotspot и hyperfine, помогает точно выявлять узкие места, без которых совершенствование было бы невозможным. Заключение можно сделать такое: оптимизация решения судоку через классический DLX алгоритм на Zig открывает горизонты высокопроизводительных вычислений в сфере комбинированных головоломок и других сложных задач точного покрытия. Применение структур данных с указателями, пакетное выделение памяти, отказ от рекурсии в некоторых местах наряду с правильным профилированием позволяют добиться результата, который превосходит многие существующие решения на популярных языках.
Это вдохновляет продолжать изучение таких методов и применить полученные знания в других сферах, от распределённых вычислений до игр и научных задач, где точное покрытие и поиск с ограничениями играют ключевую роль.