Круг и гипербола на одном графике: визуализация комплексных собственных значений и их роль в линейной алгебре

Технология блокчейн Юридические новости

В мире математики визуализации играют важную роль, помогая не только понять сложные концепции, но и расширить интуицию о поведении функций и структур. Особенно интересной является ситуация, когда на одном графике соседствуют две фундаментальные геометрические фигуры — окружность и гипербола. В чем заключается суть такого построения и какую информацию можно извлечь из этого для изучения свойств матриц с комплексными собственными значениями? Рассмотрим подробно уравнение и его геометрическую интерпретацию, а также практические применения в анализе динамических систем и линейной алгебры. Основная формула, лежащая в основе построения графика с окружностью и гиперболой, выглядит следующим образом: x² + (y + z i)² = 1. Здесь переменные x, y и z — вещественные числа, а i — мнимая единица, удовлетворяющая равенству i² = -1.

При расширении и разделении этого комплексного уравнения на вещественную и мнимую части мы получаем два уравнения: x² + y² - z² = 1 (вещественная часть) и yz = 0 (мнимая часть). Последнее условие требует, чтобы произведение y и z было равно нулю. Из него выплывает два возможных варианта: либо y = 0, либо z = 0. Рассмотрим первый вариант, при котором y = 0. Подстановка этого условия в уравнение вещественной части даёт x² - z² = 1.

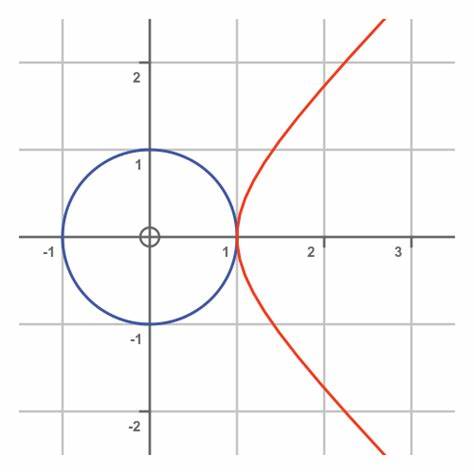
Это уравнение гиперболы в плоскости, заданной осями x и z. Гипербола представляет собой одну из классических конических секций, характеризующихся двумя ветвями и определенной асимптотикой. Второй вариант возникает при условии z = 0. Тогда уравнение переходит в форму x² + y² = 1, что является уравнением единичной окружности в плоскости x и y. Таким образом, анализ уравнения x² + (y + z i)² = 1 на плоскости трехмерного пространства с координатами x, y, z даёт в результате объединение гиперболы и окружности, локализованных в различных плоскостях.

Но почему подобное построение важно и какие выводы из него можно сделать в применении к теории матриц и динамических систем? Ответ кроется в связи с комплексными собственными значениями матриц, зависящих от параметра, который изменяется в реальной области. Так, например, рассмотрим двумерную матрицу с параметром μ: M(μ) = [0, 1 + μ; 1 - μ, 0]. Изучение собственных значений данной матрицы сводится к решению характеристического уравнения, которое по своей форме оказывается близким к уравнению x² + λ² = 1, где λ — собственное значение, а μ выступает в роли x. При введении комплексного собственого значения λ = y + z i данное уравнение полностью повторяет формулу x² + (y + z i)² = 1, что именно соответствует ранее рассмотренному графику. Отсюда можно проанализировать, как меняется природа собственных значений в зависимости от параметра μ.

Если |μ| < 1, собственные значения матрицы оказываются вещественными и относятся к разным знакам, что влияет на устойчивость и поведение динамической системы. При |μ| > 1 собственные значения становятся комплексно-сопряжёнными, а на границах μ = ±1 наблюдается кратный собственный корень λ = 0. Такая геометрическая интерпретация помогает интуитивно понимать изменения в структуре решений и их сопряжённые параметры. Кроме того, подобный подход не ограничивается лишь этой конкретной матрицей и может расширяться на другие случаи, когда матрица зависит от одного параметра и имеет комплексные собственные значения. Еще один интересный пример — матрица вида: M(μ) = [1, μ; 1, 1].

При решении характеристического уравнения для этой матрицы выясняется, что собственные значения λ удовлетворяют уравнению λ² - 2λ + (1 - μ) = 0. Выполнив замену λ = y + z i и указав μ = x, можно представить это уравнение в форме ((y + z i) - 1)² = x. После разделения на вещественную и мнимую части получается система уравнений, аналогичная предыдущему случаю, но приводящая к параболическим графикам в плоскостях xz и xy. Сама по себе визуализация этих уравнений с объединением геометрических фигур — кругов, гипербол, парабол — отличается не только эстетической привлекательностью, но и огромной образовательной ценностью. Она позволяет математике обрести наглядность, а также раскрывает фундаментальные взаимосвязи между линейной алгеброй, комплексным анализом и теориями динамических систем.

Важно подчеркнуть, что такие графики сегодня доступны благодаря современным интерактивным инструментам визуализации, например, Desmos, которые позволяют строить сложные поверхности и сечения с использованием комплексных чисел и параметрических зависимостей. Это в значительной мере способствует популяризации предмета и облегчает восприятие сложных концепций для студентов и ученых. Таким образом, единство круга и гиперболы на одном графике становится символом единства различных математических разделов: геометрии, алгебры и анализа. Осознание того, что линии, формирующие единичную окружность и гиперболу, описывают поведение собственных значений матриц, помогает создавать новые методы исследования устойчивости и переходов между типами решений динамических систем. Подводя итог, можно сказать, что исследование уравнения x² + (y + z i)² = 1 не только предлагает удивительный пример синтеза геометрических фигур, но и раскрывает двери к глубокому пониманию свойств реальных параметрически зависящих матриц и их комплексных собственных значений.

Эти знания оказываются полезными при анализе динамики систем, разработке алгоритмов и в других областях прикладной математики, инженерии и физики.