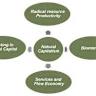
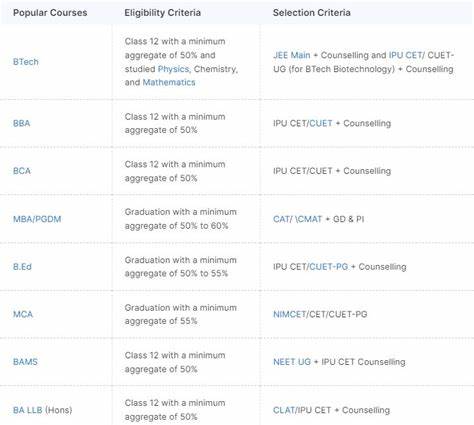
Современный мир переживает глубокие экономические и социальные изменения, которые все чаще поднимают вопросы о будущем капитализма и о том, каким образом может выглядеть посткапиталистическое общество. Традиционные представления о рыночных механизмах, прибыли и собственности подвергаются переосмыслению, а вызовы глобализации, цифровизации и экологического кризиса стимулируют дискуссии о необходимости новых структур. В этом контексте идея математического доказательства структуры посткапитализма вызывает особый интерес, поскольку она предлагает формализованный и объективный подход к пониманию альтернативных моделей организации общества и экономики.Математика, будучи универсальным языком, способна выявлять закономерности и структурные принципы в самых разных системах — от физики до биологии и социальной динамики. Если посткапитализм можно представить как набор взаимосвязанных процессов и отношений, то математические методы могут помочь выявить фундаментальные правила, управляющие этой системой.
Это позволит избавиться от субъективных интерпретаций и гипотез, переведя обсуждение в сферу строгой научной доказательности.Одним из ключевых аспектов является построение модели, которая отражает обмены ресурсами, распределение благ и формы коллективного участия в экономике нового типа. Задача состоит не только в описании параметров, но и в доказательстве устойчивости такой системы, ее способности адаптироваться к внешним изменениям и способствовать развитию человеческого потенциала. Сегодня в науке появляются работы, использующие теорию игр, вычислительную экономику, сетевые анализы и динамические системы, которые тесно связаны с данной проблематикой.Реализация математической структуры посткапитализма связана с концепцией кооперативных и децентрализованных моделей, включая платформенные экономики, распределенные реестры и пэр-ту-пэр (peer-to-peer) системы.
Именно их исследование позволяет заложить фундамент будущей экономики, которая не опирается на центральное управление и монетарные стимулы в традиционном понимании, а строится на сотрудничестве, взаимном вкладе и распределении. Доказательство, что подобная модель может не только существовать, но и быть стабильной в долгосрочной перспективе, даст мощный импульс для практической реализации таких идей.Интересным направлением является использование математического анализа сходимости и устойчивости, который традиционно применяется в инженерии и естественных науках, для доказательства того, что новая социально-экономическая структура способна сохранять равновесие и справедливость. Например, можно рассматривать эволюционные алгоритмы и методы оптимизации, которые демонстрируют стабильное улучшение качества жизни участников системы без экспоненциального роста неравенства или кризисных сбоев. Подобные исследования открывают перспективы к построению не просто утопических, а практически реализуемых структур посткапиталистической экономики.
Еще одна важная связь — это связывание структуры посткапитализма с биологическими системами и закономерностями организованной коллективной жизни. Математика биологических процессов, таких как саморегуляция, развитие и адаптация, может служить ключом к пониманию, каким образом социальная организация будущего будет работать на принципах гармонии и взаимопомощи. Подобные модели учитывают разнообразие и уникальность каждого участника системы, но при этом обеспечивают её целостность и согласованность действий.Вызовы реализации математического доказательства не ограничиваются только вычислительной и теоретической сложностью. Очень важным остается вопрос перевода полученных результатов в практические рекомендации и механизмы, которыми смогут воспользоваться общества и государственные институты.
При этом важно сохранить гибкость и открытость модели, чтобы она учитывала культурные, исторические и географические различия, а не была догматичным универсализмом.Потенциальные выгоды от успешной формализации структуры посткапитализма многочисленны. Во-первых, это повышение доверия к новым экономическим моделям, основанное на строгих доказательствах и прозрачных принципах. Во-вторых, математические модели могут способствовать оптимизации распределения ресурсов, минимизации конфликтов и устойчивому росту без разрушительных для экологии и социальной сферы последствий. В-третьих, они создают платформу для международного сотрудничества и обмена знаниями, что крайне важно в эпоху глобальных вызовов.
Однако стоит помнить, что экономика и общество — это динамичные и многогранные системы, в которых всегда присутствует элемент непредсказуемости и человеческого фактора. Математика не заменит эти реалии, но может значительно улучшить понимание и управление ими. За счет формальных моделей возможно будет разработать гибкие механизмы обратной связи и адаптивного реформирования, что обеспечит стабильность в нестабильных условиях.Несмотря на возможные сложности, идея математического доказательства посткапиталистической структуры продолжает набирать популярность среди ученых и практиков. Уже сейчас появляются проекты, которые интегрируют различные дисциплины — экономику, социологию, компьютерные науки — для создания целостных моделей.