Новый взгляд на задачу аппроксимации плоскости в 3D пространстве

Институциональное принятие

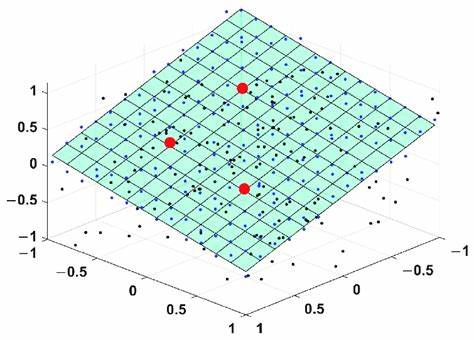
Аппроксимация плоскости в трехмерном пространстве — важная и часто встречающаяся задача в области компьютерного зрения и обработки 3D-данных. Будь то определение поверхности земли в LiDAR-сканах или выделение важных плоскостных структур в сценах, умение корректно и эффективно подбирать плоскость по набору точек является незаменимым навыком для инженеров и исследователей. Несмотря на обилие классических методов, современный подход с использованием оптимизации на многообразиях и параметризации через вращения открывает новые перспективы для решения задачи с большей гибкостью и надежностью. В данной статье мы рассмотрим традиционные и нестандартные методы аппроксимации плоскости, разберем их преимущества и недостатки, а также подробно остановимся на концепции оптимизации нормалей плоскости в пространстве SO(3). Традиционный подход к аппроксимации плоскости базируется на параметризации плоскости через нормаль и расстояние.

Плоскость в 3D пространстве можно описать уравнением, где вектор нормали представлен в виде единичного вектора, а параметр d — это смещение вдоль нормали. Для набора точек x на плоскости уравнение принимает вид: n^T * x + d = 0. При этом возникает двусмысленность, так как при замене вектора нормали на противоположный и одновременном изменении знака d плоскость не меняется. Обычно для решения задачи находят центр масс точки и сдвигают облако точек так, чтобы оно было с нулевым средним. Затем вычисляют ковариационную матрицу и выполняют метод главных компонент (PCA) для поиска направлений максимальной дисперсии.

PCA позволяет выделить подпространство с наибольшей вариативностью данных, а в случае плоскости мы ожидаем обнаружить два крупных собственных значения и одно минимальное, соответствующее направлению нормали. Такой подход прост в реализации, интуитивно понятен и хорошо работает на чистых данных без больших выбросов, однако имеет ряд ограничений. Одним из главных недостатков метода PCA является чувствительность к выбросам. Для борьбы с ними традиционно используют алгоритм RANSAC, который итеративно подбирает модели плоскостей, исключая шумные точки, однако это влияет на скорость и требует более сложной настройки. Кроме того, PCA не позволяет гибко интегрировать априорные знания и веса точек, что может быть полезно в некоторых бизнес- и инженерных задачах.

Из-за этого появляется необходимость в более универсальном и мощном инструменте, способном объединять в себе удобство оптимизации и устойчивость к шумам и выбросам. Вместо замкнутых решений классического анализа можно поставить задачу аппроксимации плоскости в виде задачи нелинейной минимизации невязок. Хорошей идеей является использование функции невязки между точкой и плоскостью, выраженной через разницу проекции точки на нормаль плоскости и параметр смещения. Целевая функция при этом принимает вид суммы квадратов таких разниц для всех точек. Однако напрямую оптимизировать нормаль с условием единичной нормы вектора — сложная задача с ограничениями, которую неудобно решать классическими методами оптимизации.

Чтобы нивелировать ограничения, становится актуальной идея оптимизации на многообразиях — математических пространствах, в которых параметры удовлетворяют определенным условиям. В частности, единичный вектор нормали лежит на сфере S2, обладающей сферической геометрией, но при этом не являющейся группой Ли, что создает определенные трудности в традиционной оптимизации. Тем не менее можно использовать структуру вращений в трехмерном пространстве, которые образуют группу Ли SO(3), для параметризации нормали. Можно взять фиксированный исходный вектор, например, направленный вдоль оси Z, и с помощью вращения задать новую нормаль. Эта вращательная параметризация избыточна, так как вращение вокруг исходной оси не изменяет вектор, соответственно одна степень свободы из трех не влияет на нормаль.

Такой подход избавляет от необходимости явно задавать ограничение нормы, поскольку вращение всегда сохраняет длину вектора. Оптимизация сводится к работе с двумя параметрами, задающими вращение в плоскости, перпендикулярной базовому вектору, и скалярному смещению плоскости d. Ключевым достоинством этого метода становится возможность применения стандартных алгоритмов нелинейной оптимизации, таких как метод Гаусса-Ньютона, в которых легко вычислять производные и строить якобианы. Это облегчает интеграцию задачи подгонки плоскости в более крупные системы калибровки и вычислительной геометрии, где параметры могут быть оценены одновременно и с использованием весов или априорных знаний. Кроме того, такая формулировка естественным образом поддерживает использование робастных функций потерь, позволяющих эффективно бороться с выбросами и шумами, не прибегая к вычислительно дорогим алгоритмам типа RANSAC.

Возможность привлечь современные численные библиотеки, например SciPy в Python, дополняет практическую ценность данного подхода. Помимо прочего, метод открывает путь для совместной оптимизации параметров точек и плоскости, что особенно актуально при восстановлении структуры из разнородных сенсорных данных с неопределенностями. Несмотря на непрямую связь пространства нормалей S2 с группой SO(3), использование вращений как инструмента управления ориентировкой позволяет обойти теоретические ограничения и добиться эффективной оптимизации. Такой подход гармонично вписывается в современную парадигму компьютерного зрения, опирающуюся на теорию многообразий и групп Ли, и способствует созданию более гибких и мощных методов решения задачи подгонки плоскости. Статья также приводит наглядные иллюстрации и демонстрации сгенерированных точек, результаты аппроксимации классическим и современным методами, а также показывает, как простое добавление робастных функций потерь значительно повышает качество результата при наличии выбросов.

В заключение стоит отметить, что подход оптимизации на многообразиях не только позволяет эффективно и точно решать задачу аппроксимации плоскости, но и расширяет горизонты методов калибровки и обработки 3D-данных в целом. Последующие исследования будут посвящены более глубокому изучению оптимизации непосредственно на сфере S2, что откроет еще более тонкие возможности для анализа и интерпретации 3D-ориентировок. Инженеры, работающие с 3D-данными, могут извлечь существенную пользу из интеграции таких методов в свои системы, добиваясь большей устойчивости, точности и функциональности. Таким образом, пересмотр классических подходов к подгонке плоскости с использованием современных математических инструментов показывает, что даже широкоизвестные задачи могут получить свежие решения с улучшенными характеристиками и широкими перспективами практического применения.