Век цифровых технологий требует надежных способов защиты данных и конфиденциальности общения. Алгоритм Диффи-Хеллмана стал одним из важнейших открытий в области криптографии, позволив обеспечить безопасный обмен ключами через открытые каналы связи. Понимание принципов работы этого алгоритма сегодня крайне важно для специалистов в области информационной безопасности, а также всех, кто интересуется устройством современных систем шифрования. Алгоритм Диффи-Хеллмана впервые был представлен в 1976 году Whitfield Diffie и Martin Hellman. Они предложили революционную идею — возможность двух сторонам обменяться секретной информацией, даже если они не знакомы и общаются через открытый канал, доступный для посторонних.
Это был прорыв, который изменил подход к защите информации, положив начало эре асимметричного шифрования, или криптографии с открытыми ключами. До появления алгоритма Диффи-Хеллмана все методы защиты строились на симметричных шифрах, где одна и та же секретная информация — ключ — использовалась для шифровки и расшифровки данных. Проблема заключалась в безопасной передаче этого ключа между отправителем и получателем. Нужно было найти способ обменяться ключом, не передавая его напрямую, чтобы избежать перехвата злоумышленниками. Диффи и Хеллман впервые предложили использовать односторонние вычислительные функции, которые можно легко выполнить в одном направлении, но крайне сложно повернуть назад.
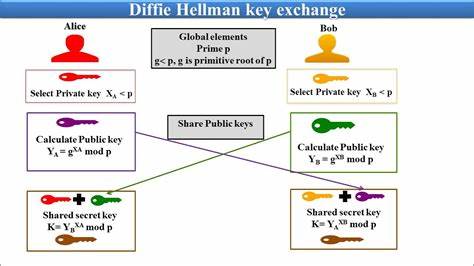
Это дало возможность сторонам сгенерировать общий секретный ключ на основе обмена публичными данными, которые могут быть доступны любому, включая злоумышленников. Принцип алгоритма основан на математической операции возведения числа в степень по модулю простого числа. Публично договариваются два параметра — большое простое число и основание (генератор). Каждая сторона самостоятельно выбирает секретное число и вычисляет публичное значение, которое отправляется другой стороне. Несмотря на то, что эти публичные значения известны всем, секретные числа остаются скрытыми.
Например, если взять маленькое простое число 13 в качестве модуля, а генератором будет число 11, и если одна из сторон выберет секретное число 5, а другая — 6, они смогут обменяться вычисленными значениями, не раскрывая своих секретов. Затем каждая сторона применяет к полученному от партнера публичному числу свою секретную степень по модулю простого числа, и в результате обе стороны получают одинаковое секретное число. Именно оно и становится общим ключом для дальнейшего симметричного шифрования. Это математическое преобразование основывается на сложности решения задачи дискретного логарифмирования, которая актуальна до сих пор. Для злоумышленника крайне проблематично, практически невозможно, вычислить исходный секрет по известным публичным данным, особенно если используются большие числа, состоящие из сотен и тысяч бит.
Таким образом, алгоритм обеспечивает надежный способ договориться о секретном ключе в открытом пространстве без риска его перехвата. Эта процедура значительно упростила использование защищенных каналов связи и позволила создавать более масштабные и безопасные информационные системы, включая интернет. Современные реализации Диффи-Хеллмана используют ключи длиной от 2048 бит, что делает их практически неприступными для вычислительных атак с использованием обычных или даже мощных серверов. Несмотря на это, угроза со стороны квантовых компьютеров, которые в перспективе могут ускорить решение дискретного логарифма, заставляет специалистов искать новые криптографические методы, устойчивые к квантовым вычислениям. Кроме того, важно понимать, что безопасность алгоритма зависит не только от математического аппарата, но и от корректной реализации в программном обеспечении и аппаратуре.
Уязвимости могут появляться из-за так называемых сайд-канальных атак — попыток получить секретные данные по косвенным параметрам работы устройства, например, по времени обработки или потреблению энергии. Алгоритм Диффи-Хеллмана, несмотря на свою возрастную историю, и по сей день остается краеугольным камнем криптографии и лежит в основе множества современных протоколов. Например, в протоколах TLS для защиты интернет-соединений, в VPN-технологиях и системах обмена сообщениями с сквозным шифрованием. Его уникальность в том, что он опроверг устоявшееся мнение, что секретные ключи должны передаваться или храниться закрыто. Использование открытых ключей дало начало новым направлениям криптографии и вдохновило создания таких алгоритмов, как RSA и эллиптические кривые, которые сегодня применяются в широком спектре приложений.
Для разработчиков и специалистов в области безопасности понимание принципов Диффи-Хеллмана необходимо для создания надежных систем и принятия обоснованных решений при построении защищенных коммуникаций. Алгоритм хорошо интегрируется с современными методами симметричного шифрования, обеспечивая баланс между эффективностью и безопасностью. Интернет и цифровая коммерция сегодня трудно представить без возможности безопасной обмена информацией, и вклад Диффи-Хеллмана в формирование этой реальности невозможно переоценить. Его концепция демонстрирует мощь математики в решении практических задач и продолжает влиять на развитие технологий, обеспечивая защиту наших данных в постоянно растущем цифровом мире.