В современном мире данные играют ключевую роль в развитии технологий, науки и бизнеса. Одной из наиболее перспективных областей является работа с так называемыми знаниями графами — специализированными базами данных, структурированными в виде простых предложений или «троек». Они помогают моделировать сложные взаимосвязи между объектами, что становится особенно востребованным в сфере искусственного интеллекта и машинного обучения. Понимание сущности знания графов и задач, связанных с прогнозированием новых связей внутри них, критично для многих исследовательских и прикладных направлений. Одним из таких направлений является концепция структурного выравнивания, которая базируется на анализе структуры графа для повышения качества предсказаний.
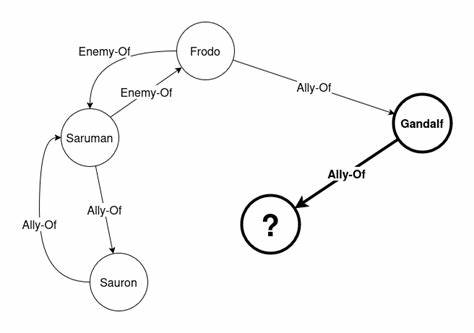
Знания графов — это прежде всего способ представления информации в виде набора троек, где каждая из них состоит из трех компонентов: субъекта, предиката и объекта. Например, в предложении (Арагорн, союзник, Фродо) «Арагорн» выступает субъектом, «союзник» — предикатом, а «Фродо» — объектом. Такое представление данных позволяет формировать сложные сети понятий, которые удобно визуализировать и анализировать. В визуальном представлении знания графы выглядят как набор связанных между собой узлов и рёбер, где каждый узел соответствует отдельному понятию или объекту, а рёбра отражают тип взаимоотношения между ними. Такая структура помогает заметить ключевые элементы сети и их взаимосвязи, а также определить степень важности или центральности отдельных компонентов.
Задача прогнозирования связей является центральной в работе с знаниями графами. Она предполагает выявление новых, логически обоснованных отношений на основе уже существующих данных, что позволяет дополнить и расширить базу знаний. Прогнозирование может происходить в двух основных вариантах: либо определяется, какой субъект следует подставить в известное отношение с объектом, либо наоборот — какой объект подходит для заданного субъекта и отношения. Рассмотрим пример: если в графе уже есть сведения о том, что «Арагорн» — союзник «Фродо» и что «Фродо» — враг «Саурона», то прогнозирующая система сможет предположить, что «Арагорн» вероятно является врагом «Саурона». Это не просто поиск информации, а полноценный интеллектуальный вывод, который позволяет открывать ранее неизвестные факты и строить новые связи.
Важность задач прогнозирования проявляется в различных сферах, но особенно ярко она прослеживается в биологических науках. Биология изобилует сложными взаимодействиями между лекарствами, заболеваниями и биологическими процессами, которые удобно моделируются с помощью знания графов. К примеру, каждая тройка может описывать связь между препаратом и заболеванием, например, (лекарство, лечит, заболевание). Поскольку многие лекарства воздействуют на несколько заболеваний, задача прогнозирования помогает выявить потенциальные лечебные эффекты, которые раньше не были открыты пациентам и исследователям. Современные фармацевтические компании активно используют такие технологии для поиска новых направлений терапии, сокращения времени разработки препаратов и повышения эффективности лечения.
Именно на этих перспективах базируется интерес к усовершенствованию методов прогнозирования в знаниях графах. Структурное выравнивание представляет собой инновационный подход к решению задачи прогнозирования связей. В основе его лежит анализ топологической структуры графа, выявление повторяющихся паттернов и локальных конфигураций, которые служат индикаторами вероятных новых связей. Такой подход отличается от классических методов тем, что он учитывает степень взаимовлияния соседних узлов и глубокую организацию графа, а не только отдельные тройки. Это позволяет повысить точность прогнозов и расширить спектр выявляемых связей.
Концепция структурного выравнивания опирается на идею, что определенные структурные сходства между частями графа предполагают похожие отношения и в других участках. Таким образом, изучение таких структурных соответствий становится мощным инструментом для предсказания новых данных на основе уже имеющейся информации. Помимо биологии, применение концепции знания графов и структурного выравнивания находит отклик в разных отраслях. В области социальных сетей эти методы помогают выявлять скрытые связи и формировать рекомендации, способствуя развитию персонализированных сервисов. В промышленности и логистике они оптимизируют процессы путем выявления взаимосвязей между элементами производства и поставок.
В организациях, занимающихся анализом больших данных и искусственным интеллектом, понимание структуры графов и методика прогнозирования позволяют создавать интеллектуальные системы, способные учиться и адаптироваться, улучшая качество решений с течением времени. Во всех этих случаях важнейшей задачей становится создание моделей, способных эффективно использовать структурную информацию для поиска новых знаний и связей. Здесь на сцену выходит структурное выравнивание как ключевой метод, который раскрывает потенциал графа максимально полно. Несмотря на сложность структурного анализа, такой подход становится доступнее благодаря развитию вычислительных возможностей и появлению новых алгоритмов машинного обучения, способных работать с графовыми структурами. Среди них выделяются графовые нейронные сети, которые интегрируют информацию о локальных и глобальных свойствах графа для точного предсказания.
Структурное выравнивание способствует развитию этой области, предоставляя гибкие и эффективные инструменты анализа. В целом, знание графов и прогнозирование связей — это фундаментальные понятия, формирующие современные интеллектуальные системы анализа данных. Применение этих концепций позволяет исследовать огромное пространство возможных отношений, открывать новые научные горизонты и создавать коммерчески успешные продукты. Структурное выравнивание — это шаг вперед в обеспечении точности и надежности таких систем. С его помощью возможно не только распознавать уже существующие данные, но и делать качественные прогнозы на основе структурных закономерностей.