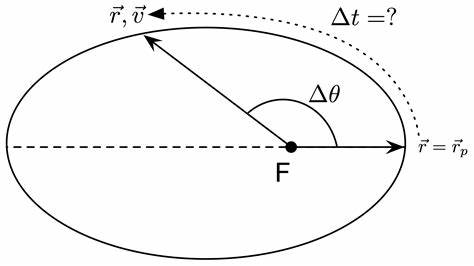
Проблема Кеплера занимает особое место в истории науки и математике, являясь классической задачей механики, связанной с движением тела под действием центральной силы, обратно пропорциональной квадрату расстояния. Эта задача получила название в честь Иоганна Кеплера — выдающегося ученого XVII века, который сформулировал основные законы движения планет. Однако современное понимание этой проблемы выходит далеко за рамки классической небесной механики, затрагивая такие области, как квантовая теория поля, спектроскопия атомов и даже структура периодической таблицы элементов. В данной статье будет освещена суть задачи Кеплера, исторические этапы её развития, а также современные математические и физические интерпретации, открывающие перспективы для дальнейших исследований. В самом классическом варианте задачи Кеплера речь идет о системе из двух тел, одно из которых значительно тяжелее другого — например, планета и солнце или электрон и ядро атома.
Центральной особенностью этой задачи является закон движения, согласно которому сила, действующая на легкое тело, направлена по линии, соединяющей тела, и по модулю обратно пропорциональна квадрату расстояния между ними. Благодаря этому свойству можно определить потенциальную энергию системы, а также консервативные величины, которые сохраняются во времени — такие как энергия, угловой момент и, что особенно интересно, вектор эксцентриситета, часто называемый в современной литературе в честь нескольких исследователей в области механики и физики, включая Лапласа, Рунге, Ленца и других. Вектор эксцентриситета, или вектор Рунге–Ленца, представляет собой особый вектор, величина которого равна эксцентриситету орбиты тела, а направление указывает к периапсиусу — ближайшей точке орбиты к центру притяжения. Его сохранение является одним из ключевых свойств задачи Кеплера и отражает высокую степень симметрии в этой системе. Именно благодаря этому вектору можно классифицировать орбиты: если его величина меньше единицы, орбита имеет форму эллипса; равна единице — параболы; больше единицы — гиперболы.
Исторически интересно, что этот вектор был сформулирован и изучен ещё задолго до появления современной теории. Писания XVIII века уже отражали знание о подобном векторе, однако подлинное понимание его природы связано с развитием механики и векторного анализа в XIX и XX веках. Учёные, такие как Якоб Герман, Иоганн Бернулли, а позже Лаплас и Рунге, сыграли важную роль в описании свойств данной величины. В XX веке эта концепция была интегрирована в так называемую «старую квантовую механику» Борна и Зоммерфельда, что позволило объяснить спектры водородного атома до появления современной квантовой механики. С математической точки зрения задача Кеплера характеризуется наличием 7 сохраняющихся величин: полной энергии, трех компонент вектора углового момента и трех компонент вектора эксцентриситета.
Однако эти величины связаны между собой и не являются абсолютно независимыми. Из всех этих консервативных свойств вытекает глубокая геометрия движения частиц в центральном поле — движение ограничено плоскостью, а траектории имеют форму хорошо известных конических сечений. При помощи векторного и тензорного анализа можно доказать сохранение каждого из этих векторов и определить взаимосвязь между ними, что открывает путь к более глубокой симметричной структуре задачи. Возникает естественный вопрос, можно ли обобщить эту задачу на пространства с произвольным числом измерений. В классическом виде обратный квадрат действует лишь в трехмерном пространстве, что связано с особенностями закона гравитации и электростатического взаимодействия.
Тем не менее исследователи стремятся изучить аналоги задачи Кеплера в высоких измерениях, что приводит к интересным математическим объектам, включая сферические симметрии и группы вращений в четырех и более измерениях. Эти исследования связаны с изучением спектров гамильтонианов и расширяют понимание таких систем в контексте теории групп Ли и их представлений. Современные исследования показывают, что фундаментальные свойства задачи Кеплера находят отражение и в квантовой теории поля, где классические консервативные векторы становятся операторами, отвечающими за сохранение определённых квантовых чисел. Это обстоятельство используется при изучении атомных спектров, а также для построения моделей, объединяющих квантовую механику и теорию относительности. В некоторых подходах рассматриваются связи между теорией связи элементов таблицы Менделеева и квантовыми полями, что отражает глубокие симметрии природы и способствует развитию теоретической химии.
Помимо теоретических аспектов, математические инструменты задачи Кеплера применяются и в астрофизике, например при моделировании орбит искусственных спутников, межпланетных миссий и взаимодействии тел в системе Земля-Луна-Солнце. Знание о консервативных свойствах орбит и о взаимосвязях между векторами углового момента и эксцентриситета помогает точно прогнозировать траектории и строить оптимальные маршруты космических аппаратов. Интересен взгляд на проблему с точки зрения современной дифференциальной геометрии и симплектических структур. Исследователи, такие как Жан-Мари Соруи, продемонстрировали, что множество решений задачи Кеплера является симплектическим многообразием, которое связано с коадъюнктными орбитами специфических групп Ли. Это способствует использованию продвинутых методов геометрической механики для анализа и интегрирования уравнений движения, а также выявлению дополнительных скрытых симметрий системы.
Исследования в области квантования задачи Кеплера приводят к интересным открытиям. Например, спектр гамильтониана Кеплера для электронов в атоме водорода можно интерпретировать как набор уровней, каждый из которых связан с определенными представлениями группы специальных вращений в четырех измерениях. Эти теории расширяют возможности квантовой механики и могут применяться для построения математических моделей и объяснения наблюдаемых физических явлений. В целом задача Кеплера является уникальным переплетением классической механики, векторного анализа, теории групп и квантовой физики. Благодаря её фундаментальной роли в понимании движения тел и симметрий, она продолжает вдохновлять как математиков, так и физиков.
Исследование этой задачи не только углубляет знания о динамических системах, но и способствует появлению новых методов в различных областях естественных наук, включая астрофизику, квантовую механику и химическую физику. В заключение, проблема Кеплера представляет собой не просто историческую задачу об орбитах планет, а важный ключ к пониманию сложных закономерностей природы. Её изучение помогает связать классические задачи с современными математическими теориями и экспериментальными фактами, открывая новые горизонты в научных исследованиях и практических приложениях.