Лямбда-исчисление — это фундаментальная формальная система, лежащая в основе современных функций и вычислений. Придуманное Алонзо Черчем в 1930-х годах, оно служит абстрактным языком для описания алгоритмов, функций и вычислимых процессов. Несмотря на свою кажущуюся простоту, лямбда-исчисление скрывает множество глубинных принципов и парадоксов, которые связаны с концепциями вычислимости, логической недоказуемости и даже теорией сложности. Одной из таких интересных тем является идея растущей энтропии внутри лямбда-диаграмм — визуальных представлений лямбда-выражений, которые помогают понять динамику их редукции и вычислений. Основы лямбда-исчисления построены на трех операциях: введение переменных через лямбда-абстракции, применение функций к аргументам и замена переменных в выражениях (бета-редукция).
Лямбда-диаграммы визуализируют эти операции с помощью линий и узлов, что позволяет увидеть структуру выражения и ход вычислений наглядно. Редукция в лямбда-исчислении — процесс упрощения выражения путём последовательного применения правил бета-редукции. Некоторые выражения легко сводятся к нормальной форме — точке, в которой дальше никаких редукций применить невозможно. Такие выражения называют редуцируемыми. Однако не все лямбда-диаграммы ведут себя идентично: существуют абсолютно редуцируемые выражения, которые, независимо от порядка применения редукций, приведут к нормальной форме.
Также существуют контингентно редуцируемые выражения, где путь редукции может привести либо к нормальной форме, либо зациклиться без конечной точки, в зависимости от выбранной стратегии редукции. И, наконец, есть абсолютно нердуцируемые выражения, которые ни при каком подходе не могут быть сведены к нормальному виду. Удивительно, что даже если два выражения A и B являются абсолютно редуцируемыми, их комбинированное применение A B может быть абсолютно нердуцируемым. Это иллюстрирует богатство и сложность поведения лямбда-выражений и подчёркивает, что свойство редуцируемости не всегда сохраняется при композиции функций. Связь лямбда-исчисления с классической теорией вычислимости проявляется в том, что лямбда-исчисление эквивалентно по мощности машине Тьюринга.
Следовательно, многие классические результаты о неполноте, неразрешимости и ограничениях вычислений применимы и в этой абстрактной среде. Например, невозможно создать универсальный «оракул редуцируемости» — лямбда-выражение, которое по входному диаграмме однозначно определяло бы, сводится ли она к нормальному виду или нет. В попытке построить такое выражение возникает логическое противоречие, отражающее доказательства неполноты Гёделя и неразрешимости проблемы останова. Эти ограничения тесно связаны с понятием Колмогоровской сложности, которая определяет минимальную длину программы на данном языке для генерации определённой строки. В контексте лямбда-исчисления подобной метрикой служит размер минимальной лямбда-диаграммы, которая сводится к заданному числу.
Из-за аналогии с Колмогоровской сложностью невозможно построить лямбда-выражение, которое вычисляет размер минимальной диаграммы для любого числа, что является ещё одним проявлением фундаментальной непредсказуемости и ограничения доказуемости. Одной из выразительных возможностей лямбда-исчисления является формальное определение чисел через представление Черча, где число N описывается как функция, применяющая заданную функцию N раз к аргументу. Это позволяет реализовывать арифметические операции и даже существенно более сложные конструкции, например, гипероперации, такие как экспонентация, тетрация и далее по иерархии гиперопераций. Каждое следующего действие строится как многократное применение предыдущего, что логично и лаконично выражается с помощью лямбда-выражений. При тщательном построении гиперопераций возникает проблема роста длины выражений.
Представление функций вроде ↑100 (100-й уровень гиперопераций) напрямую требует записи множества промежуточных функций, что быстро становится громоздким. Чтобы справиться с этой проблемой, вводятся вспомогательные функции, например g, которая реализует переход от операции на уровне N к операции на уровне N+1, позволяя эффективно описывать очень большие и сложные числа без раздувания записи за счёт многократного применения одного и того же механизма. На основе этих средств можно определить последовательность чисел, подобную последовательности, используемой при формировании знаменитого числа Грэма, которое отличается колоссальным ростом значений и является одним из самых больших чисел, используемых в математике. Лямбда-исчисление позволяет формально кодировать подобные сложные и большие числа, давая нам средства для описания процессов, которые выходят далеко за границы вычислимых и представимых на практике величин. Визуализация таких чисел и процессов с помощью лямбда-диаграмм превращает абстрактные конструкции в наглядные формы, позволяя увидеть структуру и взаимосвязи функций, аргументов и их применений.
При этом развертывание и beta-редукция таких диаграмм может привести к невероятным по размеру структурам, которые теоретически занимают пространство, превышающее даже астрономические масштабы наблюдаемой вселенной. В завершение стоит отметить, что лямбда-исчисление не просто важный объект теоретической информатики, но и насыщенный инструмент для понимания основ логики, вычислимости и сложности. Рассмотрение вопросов редуцируемости, создания оракулов и связей с Колмогоровской сложностью раскрывают глубокие границы того, что мы можем выразить и вычислить, подчеркивая одновременно красоту и ограничения формальных систем. А визуализация в виде лямбда-диаграмм позволяет сделать этот мир более доступным и интуитивно понятным. Понимание растущей энтропии и непредсказуемости в лямбда-исчислении открывает новые горизонты для исследователей, программистов, логиков и всех, кто интересуется фундаментальными аспектами вычислений.
От абстрактных сокращений до невероятных чисел — лямбда-исчисление продолжает оставаться ключом к разгадкам глубочайших вопросов теории компьютинга и математики.
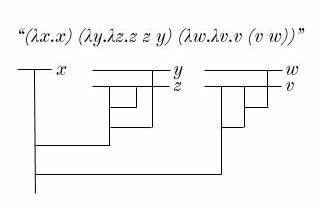




![The Slippery Slope of AI in Games – Semi-Ramblomatic [video]](/images/A85A8652-D23E-4E6A-BF46-0F1D33EB7DD7)