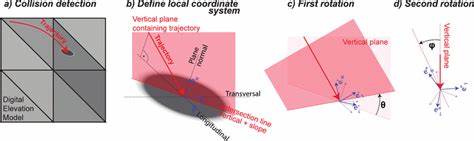
Обнаружение столкновений в трехмерной графике и компьютерных играх является одной из ключевых задач, определяющих производительность и реализм взаимодействия объектов. В последние годы разработчики и исследователи сосредоточились на улучшении алгоритмов узкой фазы коллизий, способных работать быстро и эффективно при сложных моделях с множеством граней. Одним из таких алгоритмов стал оптимизированный тест разделяющей оси (Separating Axis Test, SAT), который в сочетании с современными методами топологического обхода и анализа поддержки формирует основу поиска столкновений в трехмерном пространстве с высокой скоростью и точностью. Традиционные методы SAT основаны на вычислении проекций всех граней двух выпуклых тел на потенциальные оси разделения и проверке наличия пересечения проекций. Этот подход повышает точность, однако требует вычисления функции поддержки для каждой оси по отдельности, что приводит к значительным вычислительным затратам при больших числах граней.
Новая методика, основанная на анализе геометрической структуры и оптимизации вычислений, радикально изменяет этот процесс, позволяя сократить число вызовов функции поддержки до минимального — всего одного на запуск алгоритма, что в значительной степени ускоряет обработку. Основой понимания этого алгоритма является концепция разности Минковского двух выпуклых множеств. Разность Минковского позволяет свести задачу проверки столкновения и поиска минимального вектора раздвижки к вопросам поиска экстремальных значений поддержки на поверхности выпуклого тела, полученного путем вычитания одного множества из другого. В этом контексте функция поддержки определяет максимальное значение скалярного произведения направления и точки на границе множества, что имеет прямую геометрическую интерпретацию, связанную с расстояниями и направлениями столкновения. Для более глубокого анализа поддерживающих функций и их поведения на сфере пространства направлений вводятся понятия гауссовых карт и топологических разбиений сферы.
Гауссова карта связывает каждую грань полиэдра с нормалью, которая определяется на единичной сфере, а пересечения этих нормалей формируют ребра и вершины на сфере. Это разбиение позволяет выявить области, в которых функция поддержки постоянно определяется одним и тем же набором вершин, а ее производная меняется с переходом через границы этих областей. Таким образом, функция поддержки оказывается кусочно-дифференцируемой и ограниченной по сложным траекториям, что приводит к возникновению «изломов» — точек с разрывом производной — в местах пересечения граней. В двухмерном пространстве эти изломы соответствуют нормалям граней и являются точками на окружности, где секторы функции поддержки меняются от одного угла к другому. В трехмерном пространстве ситуация усложняется: изломы формируются не точками, а большими кругами на сфере, являющимися пересечениями плоскостей нормалей граней.
Это приводит к формированию сложного графа на сфере, вершинами которого являются пересечения таких больших кругов, а ребрами — дуги этих кругов. Именно по этому графу и происходит обход для оптимального вычисления минимального значения функции поддержки. Ключевая инновация заключается в том, что, имея начальную точку оценки функции поддержки с полным вычислением, можно последовательно переходить от одной области функции поддержки к другой, обновляя значения поддержки при пересечении границ областей без повторного полного пересчёта функции. Такой подход позволяет значительно снизить количество затрат на вычисление за счет инкрементального обновления. Одновременно с этим в основе обхода используется структура данных, напоминающая half-edge (полуребро), которая хранит топологические связи между вершинами, ребрами и гранями выпуклого тела.
Благодаря этому можно эффективно перемещаться по графу, адаптируясь к его топологии и избегая излишних вычислений. Практическая реализация данного подхода состоит в выборе стартовой нормали, для которой выполняется точное вычисление поддержки, а затем обходе по рёбрам графа сферических областей (гауссовой карты), где при пересечении с очередным ребром обновляется соответствующая вершина поддержки для нового региона. Это позволяет получить минимальное значение поддержки, которое соответствует направлению минимального вектора раздвижки в случае столкновения. Таким образом достигается не просто ускорение классического SAT, а его качественное улучшение, позволяющее работать с моделями из сотен и тысяч граней значительно быстрее. Визуализация и отладка алгоритма являются важной частью успешного внедрения.
Использование гауссовых карт и визуализация изменения функции поддержки на сфере позволяют понять устройство алгоритма, улучшить качество полигональных оболочек и предотвратить возникновение численных проблем. Особенно полезно это в комплексных физических движках и системах генерации коллизий, где точность и устойчивость играют первостепенную роль. Несмотря на очевидные преимущества, данный метод требует аккуратности в построении и поддержании данных о топологии выпуклых оболочек. Качество граней и правильное формирование реберных структур сильно влияют на стабильность и скорость работы алгоритма. Тем не менее опыт экспериментов показал, что при хорошем подборе топологии численные ошибки сводятся к минимуму и уровень производительности превосходит классические аналоги в несколько раз.