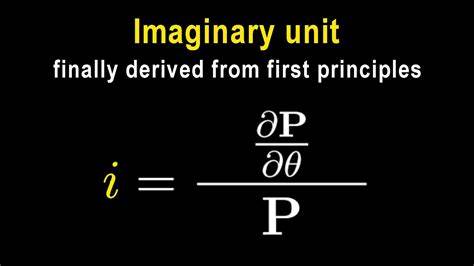Мнимая единица «i» на протяжении многих десятилетий была фундаментальным понятием в математике, особенно в области комплексных чисел. Традиционно она определялась как число, квадрат которого равен -1, что не имеет аналогов среди действительных чисел и потому названа «мнимой». Однако недавно опубликованное исследование под названием «Reimagining The Imaginary», автором которого выступает Алекс Б., помогает взглянуть на «i» с принципиально новой стороны. Эта работа ставит под сомнение устоявшиеся понятия и доказывает, что мнимая единица «i» по своей сути может рассматриваться как реальное математическое понятие, открывающее двери к новым теоретическим возможностям.
Идея исследования заключается не просто в математическом доказательстве, а в глубоком переосмыслении того, что мы называем реальным и мнимым. «i» долгое время воспринималась как абстракция, удобный инструмент для решения уравнений и математических моделей, но без собственного физического аналога или интуитивного объяснения. Алекс Б. утверждает, что такое восприятие ограничивает возможности развития математики и физики. Автор использует новаторские методы и строгий математический аппарат, комбинируя классическую алгебру с элементами криптографии и информационной теории.
Его работа криптографически защищена, что подчеркивает серьезность и ответственность подхода к утверждаемому открытию. Документ сопровождается цифровой подписью PGP и размещен на платформе Zenodo, что гарантирует его подлинность и неизменность. Доступные публично файлы, включая подробное повествование, доказательства и исходные материалы, позволяют заинтересованным специалистам самостоятельно ознакомиться с содержанием и проверить изложенные выводы. Переосмысление мнимой единицы «i» предлагает не просто новый взгляд на уже известное математическое понятие, но и открывает перспективы для решения старых проблем и создания новых математических структур. Если «i» действительно обладает реальными свойствами, это может привести к пересмотру многих фундаментальных теорий, включая те, что используются в квантовой механике, теории информации и даже в технологиях обработки данных.
Одним из ключевых моментов исследования является демонстрация того, что «мнимое» число может быть выражено и интерпретировано через реальные математические объекты, что изменяет традиционное понимание комплексных чисел. Это позволяет предположить, что границы между реальными и мнимыми числами более размыты, чем считалось ранее. Такое предположение может стимулировать разработку новых алгоритмов, оптимизаций и моделей, особенно в сферах, где комплексные числа используются как фундаментальный инструмент. Работа Алекса Б. уже привлекла внимание в научном сообществе и среди энтузиастов математики.
Несмотря на новизну и неоднозначность заявлений, многие исследователи отмечают важность попыток пересмотреть основополагающие понятия. Подобные пробелы в науке оказываются плодотворными не из-за мгновенной революции, а благодаря долгосрочному обсуждению, проверкам и интеграции новых идей в существующий научный ландшафт. Доступность публикации под лицензией Creative Commons Attribution 4.0 International способствует широкому распространению работы и ее использованию в образовательных, научных и исследовательских целях. Важной составляющей является возможность не только изучать представленные доказательства, но и принимать участие в развитии новых теорий, используя открытый исходный код и материалы, размещенные в репозитории GitHub.
Это способствует формированию сообщества вокруг идеи, где заинтересованные лица могут обмениваться мнениями, предлагать улучшения и совместно проводить эксперименты. Успех и принятие идеи о реальности мнимой единицы «i» будет зависеть от ее проверки и адаптации в практике научной деятельности. Для математики и смежных дисциплин это может стать важным этапом в эволюции понимания числовых систем и их взаимодействия с реальным миром. Впрочем, даже если концепция не станет быстро общепринятой, сама инициатива переосмысления основы знаний — это шаг к развитию и укреплению научной мысли. Таким образом, доказательство того, что мнимая единица «i» может считаться реальной, представляет собой не просто любопытное утверждение, а вызов традиционным представлениям и приглашение к исследовательской деятельности на грани математики, физики и информатики.