Создатели многих приложений часто сталкиваются с ситуацией, когда люди считают простые программы, вроде калькулятора, тривиальными и легкими в реализации. Возникает мнение, что «калькулятор – это же элементарно, кто угодно может сделать такое». Однако это далеко от истины. На самом деле разработка калькулятора высокого уровня точности и удобства – это сложнейшая задача, которая затрагивает глубинные вопросы математики, вычислительной точности и эффективности алгоритмов. На первый взгляд, кажется, что калькулятор – это просто устройство, которое принимает математическое выражение и выдает результат.
В действительности же это совсем не так. Чтобы калькулятор корректно работал и всегда показывал правильный ответ, необходимо преодолеть множество технических и теоретических трудностей. Одной из первых проблем является представление чисел внутри программы. Традиционно числа в вычислительной технике представляют либо в виде целых чисел с ограниченным диапазоном, либо в виде чисел с плавающей точкой. Но эти варианты не идеальны.
Например, числа с плавающей точкой зачастую дают ошибки округления, что приводит к неточностям. Это особенно критично, когда речь идет о сложных математических операциях с иррациональными числами, такими как пи или корень из двух. Разработчики подошли к решению этой проблемы с использованием более продвинутых математических подходов. Один из них связан с алгебраическими числами. Вместо хранения числа в виде десятичной дроби или дроби с числителем и знаменателем, предлагается хранить его как корень полиномиального уравнения с рациональными коэффициентами.
Например, корень из двух можно представить уравнением x² - 2 = 0. При этом дополнительно хранится информация, о каком именно корне идет речь – в данном случае положительном. Такой подход помогает работать с числами, которые можно алгебраически выразить, и облегчает операции сложения и умножения, используя методы из теории полиномов, например, резольвенты и композицию полиномов. Однако алгоритмы с алгебраическими числами не решают проблему полностью, так как они не охватывают трансендентные числа, например, число пи. Для работы с такими числами потребовалось перейти на более общий и глубокий уровень – так называемые конструктивные вещественные числа.
Создатели калькулятора реализовали метод, известный как рекурсивная вещественная арифметика. Смысл такого подхода в том, что каждое число представляется функцией, которая по запрашиваемой точности возвращает рациональное приближение с гарантией того, что ошибка не превышает заявленную. Таким образом можно последовательно вычислять приближения к числу с любой точностью. Например, число пи невозможно полностью представить в виде десятичной дроби, но можно запросить приближение до 0.01 и получить 3.
14, что близко к реальному значению с нужной точностью. Рекурсивная вещественная арифметика позволяет работать с широким классом чисел, включая иррациональные и трансендентные значения, и поддерживает основные математические операции и функции, такие как синусы, косинусы, экспоненты и логарифмы. Тем не менее, у этого метода есть серьезное ограничение – проблема проверки равенства чисел. Сравнение двух чисел решается путем последовательного уточнения приближений до тех пор, пока не будет найдено отличие. Но если числа равны, процесс не завершится никогда, что ставит под вопрос возможность однозначно определить, когда число равно нулю или другому значению.
Это создает сложности с отображением точных значений на экране. Например, выражение sin(π) должно строго равняться нулю, но вычислительная модель рекурсивной арифметики не позволяет точно подтвердить это, так как для этого потребовалось бы бесконечно уточнять приближения. В результате вывод на экран «0» в подобных случаях невозможен с абсолютной гарантией корректности. Чтобы преодолеть эти проблемы, команда разработчиков обратилась к исследованиям в области числовой теории и вычислительной математики. В 1990-х годах была разработана теория, описанная такими исследователями, как Дэн Ричардсон и Джон Фитч, которая позволяет упростить задачи сравнения чисел, ограничив множество операций, которые можно применять к числам.
Вместо того чтобы пытаться сравнивать любые вещественные числа, решение заключалось в том, чтобы работать с числовыми выражениями, порожденными только теми функциями и операциями, которые используются в калькуляторе: основные арифметические операции, квадратные корни, тригонометрические функции и их обратные, экспоненты и логарифмы. Это существенно ограничивало класс чисел и делало возможным сравнение и оптимизацию, но оставалась проблема производительности – алгоритмы были очень медленными и непрактичными для реальных приложений. Следующий шаг разработчиков заключался в объединении преимуществ рациональной арифметики и рекурсивной вещественной арифметики. Рациональные числа дают точные результаты, но не могут выразить такие числа, как π, а рекурсивная арифметика работает с иррациональными числами, но не дает точных ответов. Комбинация этих подходов позволяла хранить число в виде произведения рационального коэффициента и вещественной части, которая сама может быть либо рациональной, либо символической или рекурсивной.
Особое внимание уделялось организации представления символических чисел. Вместо того, чтобы хранить сотни или тысячи знаков числа pi в виде набора приближений, в приложении хранилась именно символическая константа π, которая затем могла использоваться в дальнейших вычислениях символически. Такой подход не только ускорял работу калькулятора, но и позволял сохранять математическую точность там, где это возможно. Аналогично вводились символические представления для выражений типа квадратного корня, синуса от рационального числа, логарифма и других популярных функций. В итоге разработчики получили систему, которая использовала рациональную арифметику для точных вычислений, символические представления для распространенных иррациональных чисел и локально применяла рекурсивную вещественную арифметику тогда, когда это было неизбежно.
Такая гармония обеспечивала высокую точность отображаемых результатов и делала возможным удобный пользовательский интерфейс, без бесконечных десятичных дробей и математических неопределенностей. Стоит отметить, что похожие задачи решает программное обеспечение, известное как системы компьютерной алгебры, которые могут оперировать с символическими выражениями и производить точные вычисления. Но такие системы обычно сложны и тяжеловесны, что делает их практическое применение сложным в обыденном калькуляторе. Именно поэтому интегрирование комбинированного решения стало настоящим инженерным открытием: оно сочетает точность, скорость и удобство, сохраняя при этом простоту реализации на уровне одного приложения. Таким образом, разработка обычного калькулятора, которым пользуется повседневный пользователь, на самом деле включает глубокие исследования математики, теории чисел и вычислительных алгоритмов.
Калькулятор – это не просто набор операций, а сложная система, которая балансирует между точностью, эффективностью и пользовательским опытом. Каждый раз, когда вы вводите сложное выражение и видите мгновенный и правильный результат, знайте, что за этим стоит многолетняя работа инженеров и математиков, которые сумели решить на первый взгляд непосильные задачи. В следующий раз, глядя на приложение калькулятора на вашем телефоне или компьютере, вы сможете оценить всю глубину и гений, вложенный в этот незаметный, но очень важный инструмент.
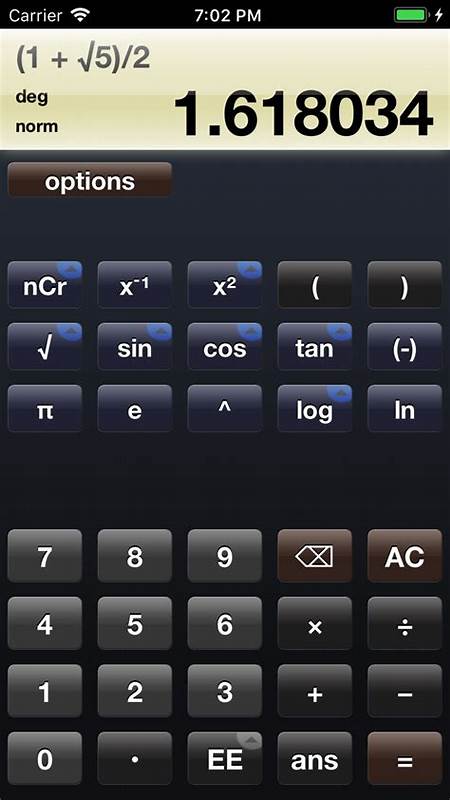



![NES Emulator from Scratch [video]](/images/505D5E3A-8221-4B3B-914B-6630C6A6847F)