Применение неравномерных сеток конечных элементов, основанных на динамике лучей, для решения задач уравнения Гельмгольца

Институциональное принятие Крипто-кошельки

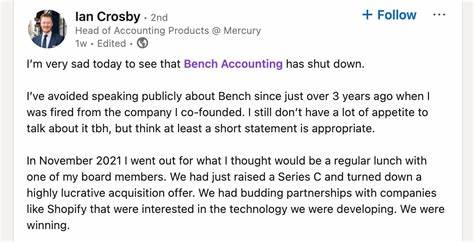
Уравнение Гельмгольца, играющее ключевую роль в математическом моделировании волновых процессов, является одной из наиболее изучаемых и одновременно сложных в численном анализе задач. Особенно это касается высокочастотных решений, где классические методы конечных элементов (FEM) сталкиваются с множеством трудностей, связанных с обеспечением точности и эффективностью вычислений. Традиционно для таких задач использовались равномерные сетки, что вызывало значительные затраты ресурсов и ограничивало применение метода в сложных сценариях. Однако недавно появившийся подход, основанный на построении неравномерных сеток конечных элементов с учетом динамики лучей, демонстрирует перспективы значительного улучшения результатов и производительности. Один из ключевых аспектов при решении высокочастотных задач уравнения Гельмгольца заключается в правильном подборе параметров конечных элементов.

Стандартные методы h-FEM (метод конечных элементов с параметром масштабирования по размеру элементов h) требуют соблюдения строгих условий, связанных с отношением между размером элемента, степенью аппроксимации и волновым числом. В частности, условие "(hk)^p ho достаточно мало" определяет, насколько мелкой должна быть сетка для обеспечения квазиоптимальности решения. При этом ho характеризует поведение решения, чаще всего пропорционально волновому числу k. Такие условия, хотя и эффективны в теории, в практике приводят к чрезмерно детализированным сеткам по всему расчетному пространству, что увеличивает вычислительную сложность. Инновационный подход, предложенный ведущими исследователями, основан на анализе поведения решения как функции свойств динамики лучей внутри области моделирования.

Идея в том, что данные для решения и его значение меняются неравномерно в различных регионах, особенно в зависимости от того, каким образом волны (лучи) распространяются внутри области и взаимодействуют с границами и препятствиями. В частности, в областях, где лучи не формируют траекторий с зацеплением (т.е. не возникает траппинга, или затормаживания волн), можно применять более грубые сетки без существенной потери точности. В то же время, в районах с интенсивной динамикой лучей или вблизи важных границ требуется более высокая детализация сетки.

Особое внимание уделяется так называемому «совершенно согласованному слою» (PML – Perfectly Matched Layer), используемому для имитации условий на бесконечности и поглощения исходящих волн без отражений. Традиционно PML также требует мелкой сетки для избежания численных артефактов, однако анализ динамики лучей показывает, что здесь можно существенно ослабить требования к размеру элементов. Результаты теоретического анализа доказывают, что в PML достаточно обеспечить малое произведение hk, без необходимости соблюдения более строгих условий с учетом степени аппроксимации p. Это снижает количество элементов в зоне PML и ускоряет вычисления. Методика базируется на совмещении современной аналитики решения уравнения Гельмгольца с продвинутыми подходами к построению сетки.

Использование информации о путях распространения лучей внутри области позволяет «нацеленно» распределять вычислительные ресурсы, делая элементы мелкими там, где волновое поле сложное и подвержено сильным колебаниям, и крупными в более простых областях. Такая стратегия обеспечивает сохранение квазиоптимальности (QO) и ограниченного относительного отклонения (BRE) одновременно с существенным сокращением числа вычислительных ячеек. Существенная теоретическая новизна исследования заключается в точном описании взаимного влияния размеров элементов в различных подрегионах расчетной области на ошибку решения в этих и прочих местах. Это расширяет существующие результаты, ранее применявшиеся только к равномерным или слабо варьируемым сеткам. Показано, что аппараты двойственности и другие современные аналитические методы позволяют балансировать локальные требования к сетке, учитывая глобальное поведение решения.

Практическая значимость данного подхода очевидна для ряда приложений. Например, в задачах акустического и электромагнитного рассеяния, где часто встречаются сложные геометрические конфигурации и затрудненная динамика волн, неравномерные сетки на основе динамики лучей позволяют упростить вычисления без потери точности. Особенно это ценится в системах моделирования реального времени, где требуется оптимальное соотношение скорости и качества расчета. Кроме того, использование данных о траекториях лучей способствует улучшению понимания физической природы волновых процессов в сложных средах. Это открывает перспективы для дальнейших исследований по адаптивному управлению сеткой в процессе решения, где сетка динамически изменяется по мере расчета, основываясь на актуальной информации о характере волн.