Понимание причинности является ключевым аспектом в изучении физических процессов и систем. В основе лежит понятие, что эффект не может предшествовать своей причине, то есть событие должно следовать за причиной во времени. Этот фундаментальный принцип находит своё отражение в формализмах линейной теории отклика, где описывается поведение систем под воздействием внешних возмущений. В рамках данной теории особое значение приобретают соотношения Крамерса-Кронига, которые устанавливают взаимосвязь между реальной и мнимой частями функции отклика, обеспечивая выполнение условия причинности. Для наглядного понимания причинности рассмотрим классический пример — движение частицы с массой в вязкой среде, под действием внешней силы.
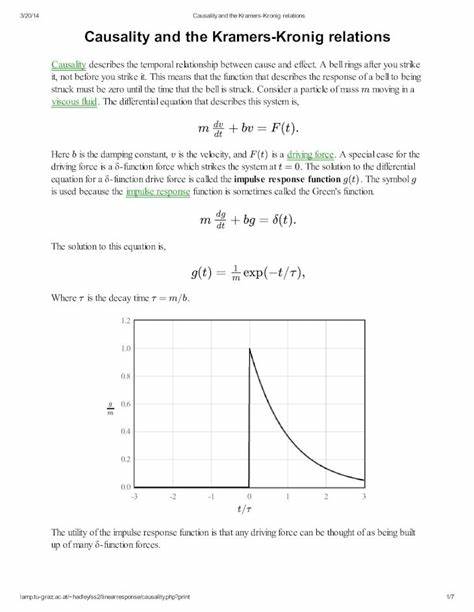
Это движение описывается дифференциальным уравнением, связывающим массу, скорость и силы трения. Важным инструментом анализа здесь выступает импульсная функция отклика — решение уравнения при δ-функции внешней силы, действующей в момент времени t=0. Импульсная функция характеризует реакцию системы, инициированную мгновенным воздействием, и обязана быть равна нулю для моментов времени до воздействия, что отражает причинно-следственную связь. Импульсная функция отклика выступает фундаментальной стройматериалом для построения отклика на произвольное внешнее воздействие. Используя принцип суперпозиции, любую сложную временную зависимость силы можно представить как сумму последовательных δ-функций, что позволяет свести вычисление отклика к свертке импульсной функции с входным сигналом.
Это математическое представление удобно для анализа систем с гармоническим возбуждением, когда внешняя сила задаётся синусоидальной функцией с определённой частотой. В этом гармоническом случае система откликается также гармонически на той же частоте, но с определённым сдвигом по фазе и изменением амплитуды. Ключевая характеристика отклика содана в виде обобщённой восприимчивости, представляющей собой отношение амплитуды отклика к амплитуде внешней силы в частотной области. Обобщённая восприимчивость связана с импульсной функцией отклика через преобразование Фурье, что позволяет переходить от временной к частотной области и наоборот. Важно отметить особенность выбора знака в фазовом экспоненте гармонической функции: в литературе используются обе формы – e^{iωt} и e^{-iωt}.
Этот выбор влияет на знак мнимой части восприимчивости, но не меняет её физического смысла. Будучи согласованным внутри анализа, данный момент не вызывает конфликтов и позволяет гибко работать с формализмом. Функция отклика, являясь нулевой для отрицательного времени, может быть разложена на чётную и нечётную части. Такое разложение иллюстрирует глубокую связь между симметрией по времени и свойствами восприимчивости в частотной области. Здесь чётная часть отвечает за реальную часть восприимчивости, а нечётная — за мнимую.
Благодаря этим связям можно восстанавливать одну часть восприимчивости, зная другую, если сохранена условие причинности. Главная ценность соотношений Крамерса-Кронига заключается именно в возможности взаимно однозначного восстановления реальной и мнимой частотных компонент восприимчивости при условии её аналитичности и выполнения условий причинности. Эти соотношения представляют собой интегральные формулы с главными значениями и обеспечивают строгий математический каркас для анализа спектральных свойств отклика. Помимо теоретической значимости, соотношения Крамерса-Кронига нашли широкое применение в различных областях физики и техники. Например, в оптике они используют для анализа комплексного показателя преломления и диэлектрической проницаемости веществ, где реальная часть отвечает за дисперсию, а мнимая — за поглощение.
Аналогично, в электротехнике и материаловедении эти соотношения помогают определить энергетические потери и реактивные параметры систем, исследовать свойства магнитных и тепловых проводимостей. Соединение между временным и частотным представлениями отклика имеет важное значение при экспериментальных измерениях. Часто измеряют только одну из составляющих — либо амплитуду, либо фазу, либо только часть спектра. Соотношения Крамерса-Кронига позволяют достоверно восстанавливать недостающую информацию и повышать точность анализа. Особое внимание уделяется практическим вопросам численного применения этих соотношений.
Стандартная форма в частотной области содержит сингулярность, что требует аккуратного обращения с интегралами и специальных методов вычисления главных значений. Временное представление, раскрывающее связь межу сопряжёнными компонентами, порой оказывается более удобным для численных алгоритмов и моделирования. Исторически соотношения Крамерса-Кронига возникли в середине XX века как мощный инструмент в линейной теории отклика и квантовой механике. Их формализм тесно переплетается с понятиями аналитичности функций комплексной переменной и принципами физической причинности, создавая мост между математическими структурами и физическими ограничениями. Их универсальность и надёжность способствовали широкому распространению в научных публикациях, учебниках и практических исследованиях.
Аналогично, причины, по которым соотношения Крамерса-Кронига приобрели статус обязательного условия для физических моделей, связаны с фундаментальными ограничениями, налагаемыми принципом причинности. Любая теория, не удовлетворяющая этим соотношениям, нарушает базовые физические конвенции и не может быть признана корректной. Обобщая, причинность в физике тесно связана с анализом линейных систем и откликов, требуя от функций отклика особой структуры по времени. Соотношения Крамерса-Кронига являются математическим воплощением этих требований в частотной области, позволяя однозначно связывать разные компоненты спектрального ответа. Их применение распространяется на электрические, оптические, магнитные и тепловые явления, обеспечивая надёжность и целостность интерпретации экспериментальных и теоретических данных.
В современном научном и инженерном мире понимание и правильное применение соотношений Крамерса-Кронига имеет огромное значение. Они служат основой для диагностики материалов, создания новых устройств с заданными свойствами и улучшения моделей взаимодействия волн и материи. Погружение в эту тему открывает доступ к глубоким закономерностям природы и расширяет горизонты применения причинного анализа во множестве дисциплин. В завершение стоит подчеркнуть, что причинность и соотношения Крамерса-Кронига представляют собой не просто абстрактные математические конструкции. Это жизненно важные инструменты, без которых невозможно полноценное понимание и описание динамических процессов в физических системах.
Освоение этих концепций — неотъемлемый шаг на пути профессионального развития исследователя, инженера или практикующего специалиста в области физики и смежных наук.