Физика часто воспринимается через призму уравнений движения и классических аналитических методов. Однако существует менее очевидный, но глубоко фундаментальный подход — принцип наименьшего действия, который рассматривает физические процессы как оптимизационные задачи. Согласно этому принципу, реальный путь системы — это такой, при котором действие достигает стационарного значения, чаще всего минимального. В традиционной физике эта задача решается с помощью вариационных методов и уравнений Эйлера-Лагранжа. Но с развитием вычислительных методов и автоматизированного дифференцирования появилась возможность применять к этим задачам численные методы оптимизации.
Одним из наиболее перспективных и интуитивно понятных методов является градиентный спуск, который позволяет искать пути наименьшего действия, минимизируя функционал действия в дискретной форме. Такая методология не только расширяет инструментарий классической механики, но и предлагает перспективы применения в сложных динамических системах, где аналитическое решение затруднено или невозможно. Основная идея принципа наименьшего действия состоит в том, что физическая система переходит из состояния начального в конечное, выбирая из множества возможных путей именно тот, для которого интеграл функции Лагранжиана — действие — принимает минимальное или стационарное значение. Функция Лагранжиана обычно определяется как разность кинетической и потенциальной энергии. Для практического применения принципа наименьшего действия традиционно выводится уравнение Эйлера-Лагранжа, решение которого дает классические уравнения движения.
Однако такой путь требует аналитических выкладок и способен работать ограниченно в сложных или хаотичных системах. Использование градиентного спуска предполагает дискретизацию временного интервала на множество малых срезов и представление пути системы как набора координат в эти моменты. Далее действие считается суммой значений Лагранжиана во всех точках, а при помощи автоматического вычисления градиента по координатам осуществляется постепенная оптимизация пути. Начальное приближение может быть практически любым — например, случайным набором положений, который затем корректируется в направлении уменьшения действия. Такой подход позволяет обойти необходимость решения дифференциальных уравнений напрямую и открыть новые возможности для моделирования непростых физических процессов.
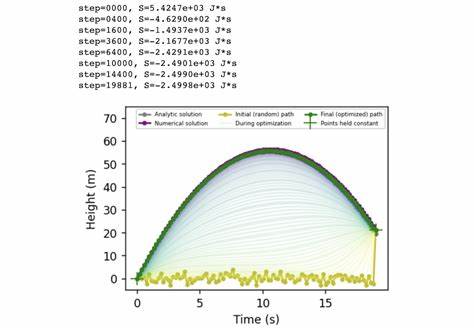
Примером для иллюстрации является движение свободного тела в гравитационном поле. Аналитически известно, что тело под действием постоянной силы тяжести движется по параболической траектории. Традиционные методы дают уравнение движения y(t) = -½gt² + v₀t + y₀. В свою очередь, численный подход через градиентный спуск начинается с произвольного набора координат и, минимизируя действие, постепенно приводит этот путь к классической параболе. Это подтверждается совпадением оптимизированного пути с результатом решения обычных уравнений с помощью численных методов и интегрирования с шагом по времени.
Преимущества использования градиентного спуска для поиска путей наименьшего действия заключаются в гибкости и универсальности. Данный метод легко адаптируется для любых систем с известным выражением Лагранжиана, включая сложные физические модели с большим числом степеней свободы, где аналитические решения либо невозможны, либо крайне сложны. Также это идеальный инструмент для исследования динамики систем с хаотическим поведением, например, в задачах многотельных взаимодействий, твердых тел, газов или даже квантовых систем, где статистические методы играют ключевую роль. Применение градиентного спуска требует аккуратного подхода к параметрам оптимизации – выбору размера шага, количества итераций и точности расчета градиентов. Слишком большой шаг может привести к расходимости, а слишком малый – к длительному времени работы алгоритма.
Важной особенностью является фиксация начального и конечного положений, поскольку эти точки задают граничные условия задачи. Именно поэтому при вычислении градиентов для крайних точек значения искусственно зануляются, чтобы первая и последняя координаты оставались неизменными. Это обеспечивает физическую корректность решения и стабильность численного метода. Использование современных библиотек автоматического дифференцирования, таких как PyTorch, значительно облегчает реализацию подобной оптимизации. Они позволяют эффективно вычислять производные по множества параметров и интегрировать этот процесс в цикл обновления решения.
Такое сочетание физически обоснованного принципа наименьшего действия и передовых вычислительных инструментов открывает новые горизонты для моделирования в физике, физической химии и инженерных дисциплинах. В математическом и физическом плане применение градиентного спуска к минимизации действия подчеркивает глубокую связь между механикой, оптимизацией и современным численным анализом. Это демонстрирует, что законы природы могут быть переформулированы как задачи оптимизации, что расширяет концептуальные рамки традиционной физики и делает ее ближе к информационным и вычислительным наукам. Перспективы развития данного подхода включают исследование более сложных систем с множественными взаимодействующими параметрами, учет квантовых и релятивистских эффектов, а также применение к задачам оптимального управления и робототехники. Методика способна интегрировать новые данные, обучаться на примерах и адаптироваться под специфические условия задачи, что открывает дополнительные возможности для междисциплинарных исследований.