Современные языковые модели удивительно эффективно справляются с одной из самых сложных задач искусственного интеллекта - представлением и обработкой огромного количества понятий и смыслов в компактных числовых пространствах. Одним из ключевых вопросов, который заинтересовал как исследователей, так и широкой технической аудитории, стало понимание того, как модели вроде GPT-3 умещают миллиарды различных концепций в пространствах с измерениями всего около 12 000. Это кажется невероятным, учитывая, что размерность пространства напрямую ограничивает количество полностью ортогональных векторов в нём. Однако реальность оказывается куда более интересной и глубокой благодаря удивительным свойствам высокоразмерной геометрии и математической теореме, известной как лемма Джонсон-Линденштраусса. В традиционных представлениях мы склонны понимать, что в N-мерном пространстве можно иметь не больше N полностью ортогональных векторов.
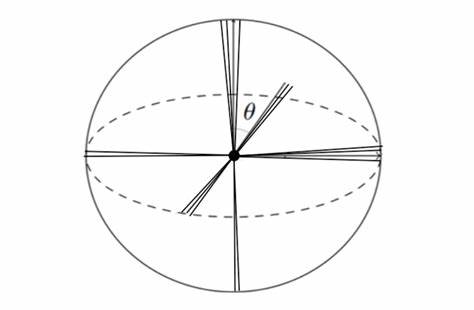
Такие векторы расположены под прямым углом друг к другу, что обеспечивает максимальную независимость между ними. Тем не менее в практике языковых моделей понятия редко бывают идеально независимы - они скорее перекрываются и частично связаны. Такая "квазииортогональность", когда векторы расположены под углами, близкими к 90 градусам, но не строго равными, существенно расширяет вместимость пространства, позволяя хранить миллионы и даже миллиарды понятий, сохраняя при этом их семантические различия. Этот феномен можно сравнить с размещением множества шаров в высокоразмерном пространстве так, чтобы они не накладывались друг на друга, но при этом были достаточно близко, чтобы сохранять взаимосвязи. Однако даже при этом процессе существуют ограничения - максимальный угол, под которым можно располагать векторы при их плотной упаковке, может быть меньше классических 90 градусов.
Эксперименты показывают, что в реальных оптимизациях угол может составлять примерно 76,5 градусов, что соответствует компромиссу между ортогональностью и вместимостью. Лемма Джонсон-Линденштраусса является ключевым математическим инструментом в понимании этих процессов. Она гарантирует, что можно проецировать точки из пространства с очень высокой размерностью в пространство с гораздо меньшей размерностью, при этом сохраняя расстояния между ними с высокой точностью. Это позволяет эффективно уменьшать размерность данных без потери важной информации, что критично для практического применения в машинном обучении, в частности - когда речь идёт о работе с миллионами концепций, каждая из которых может быть представлена как точка в высокоразмерном пространстве. Реальные применения этой леммы охватывают два важных направления.
Во-первых, это задачa снижения размерности: большой массив данных с миллионами параметров можно безопасно сжать до тысяч измерений, сохраняя при этом основные взаимосвязи между объектами. Например, в электронной коммерции каждый покупатель может быть описан вектором с миллионами параметров, что затрудняет анализ, но преобразование с помощью проекции по лемме Джонсон-Линденштраусса позволяет сократить размерность и сделать анализ эффективным и оперативным. Во-вторых, понимание ограничений и ёмкости самого пространства эмбеддингов позволяет определить, сколько понятий и семантических векторов может одновременно сосуществовать, не теряя своей уникальности и полезности для модели. Важным аспектом здесь является то, что понятия в языке и мышлении часто взаимосвязаны и имеют степень перекрытия - векторы понятий не обязательно полностью ортогональны, и это свойство позволяет дальнейшее расширение емкости через использование "квазииортогональных" отношений. Экспериментальный подход с использованием газообразного ускорения с помощью GPU-вычислений позволил исследовать верхние границы таких пространств, моделируя оптимальные способы упаковки десятков тысяч и даже сотен тысяч векторов в пространства размерности до 10 000.
Результаты показали, что реалистичные значения параметра C, влияющего на количество необходимых измерений для сохранения совпадения расстояний, могут быть существенно ниже, чем традиционные консервативные оценки. Это означает, что современные языковые модели используют пространство с гораздо большей емкостью, чем предполагалось ранее. Для примера, в GPT-3 с размерностью пространства эмбеддингов около 12 288, при небольшой степени отклонения угла от идеальной ортогональности (например, угол 87-89 градусов), количество потенциально различимых понятий прокативается от 10⁸ до впечатляющих 10⁷³ и более. Даже при консервативном подсчёте, объём представления концепций значительно превосходит количество атомов во вселенной, что открывает совершенно новое понимание того, как языковые модели могут обрабатывать сложные и взаимосвязанные знания в компактных форматах. Эти результаты существенно повлияли на понимание процесса формирования семантических представлений в трансформерах и других современных архитектурах глубокого обучения.
Они подтверждают, что не только размерность пространства, но и умение модели эффективно организовывать и оптимизировать расположение понятий в этом пространстве является критическим для качества работы. Понимание таких физических и математических пределов предоставляет новые инструменты для проектирования и оптимизации языковых моделей будущего. Оно помогает объяснить, как модели могут одновременно хранить информацию о тысячах понятий, сохраняя различия между ними, и при этом эффективно обучаться, избегая "захламления" пространства избыточно похожими представлениями. В конечном счёте, совместная работа исследователей, таких как Николас Йодер и Грант Сандерсон, вдохновлённая видеоконтентом и профессиональной дискуссией, иллюстрирует важность междисциплинарного сотрудничества и глубокого анализа теоретических основ машинного обучения, подтверждая, что фундаментальная математика остаётся основой для инноваций в области искусственного интеллекта. Для специалистов, работающих с большими данными и языковыми моделями, понимание этих принципов поможет создавать более эффективные алгоритмы, а также расширять потенциальные возможности обучения и генерации текста.
Освоение теоремы Джонсон-Линденштраусса и тонкостей высокоразмерной геометрии даёт фундаментальную базу как для теоретических исследований, так и для практических реализаций в индустрии. Таким образом, способность языковых моделей упаковывать миллиарды понятий в пространство всего с 12 000 измерений - это не магия, а результат глубоких математических свойств и инновационных инженерных решений, которые позволяют искусственному интеллекту продолжать развиваться, приближаясь к пониманию и созданию человеческого языка на качественно новом уровне. .