В последние годы диффузионные модели приобрели статус универсальных инструментов генерации высококачественных данных в самых разных областях — от создания реалистичных изображений до моделирования молекулярных структур и траекторий роботов. Их уникальная сила заключается в способности обучаться восстанавливать данные из чистого шума через серию шагов денойзинга, что придаёт выходным результатам высокую достоверность и естественность. Однако традиционные подходы с диффузионными моделями в первую очередь ориентированы на создание реалистичного визуального или структурного контента. Они менее подходят для задач, где главное — максимизировать определённую метрику или функцию награды, будь то симуляция химического связывания, оценка человеческих предпочтений или специфический показатель производительности в планировании и дизайне. Здесь классические диффузионные методы сталкиваются с трудностями, поскольку зачастую требуют дифференцируемости функции награды для эффективного guidance, что ограничивает использование сложных или блэкбокс критериев оценки.
В то же время эволюционные алгоритмы, такие как метод перекрестной энтропии (CEM) или CMA-ES, традиционно хорошо справляются с оптимизацией сложных, недифференцируемых функций, но при работе напрямую с исходным пространством объектов эти алгоритмы тратят большую часть вычислительных ресурсов на бесполезные или некорректные кандидаты. Возникает потребность в методе, который сочетает сильные стороны диффузионных моделей и мощь эволюционных стратегий, одновременно минимизируя их недостатки. Концепция Diffusion Elites (Диффузионные Элиты) предлагает элегантное и при этом удивительно действенное решение. Основная идея состоит в том, чтобы использовать предобученную диффузионную модель как приоритетное распределение в латентном пространстве и затем применять кросс-энтропийный метод для поиска эталонов высококачественных вариантов непосредственно в этом пространстве. Такой подход гарантирует, что все создаваемые кандидаты находятся на «данном многообразии» — то есть представляют собой реалистичные и валидные образцы, обеспечивая экономию ресурсов и более быстрое сходимое поведение оптимизационного процесса.
Алгоритм Diffusion Elites интуитивно прост и включает в себя последовательные этапы: из латентного пространства со стандартным гауссовским распределением выбирается популяция векторов, которые затем проходят полное преобразование через диффузионный денойзинг, получая структурированный объект. Далее каждый объект оценивается с помощью произвольной функции награды — которая может быть абсолютно «чёрным ящиком», не требующим дифференцируемости. После оценки отбирается верхний процент лучших кандидатов, по которым заново рассчитываются параметры гауссового распределения (среднее и ковариационная матрица). Обновлённое распределение задаёт основу для следующей итерации, циклически улучшая качество сгенерированных примеров и приближая поиск к оптимальной области в латентном пространстве. Преимущества Diffusion Elites выходят за рамки чисто алгоритмической простоты.
Возможность абсолютно параллельного исполнения как выборки из гауссовского распределения, так и этапов денойзинга и оценки создаёт огромный простор для масштабирования. Это делает метод практически идеальным для распределённых вычислений — можно легко запускать одновременно сотни или тысячи кандидатов, используя мощности современных GPU-кластеров или облачных сервисов. Большой плюс в том, что функция награды не ограничена градиентными вычислениями, что расширяет спектр задач, в которых можно использовать Diffusion Elites. Задействовать можно симуляторы физики или биохимии, модели мира для лонгридов, системы компьютерного зрения для анализа визуального содержания, языковые модели для семантической оценки и даже человеческие предпочтения, предсказанные через обученные модели. Метод обеспечивает гибкость, позволяя интегрировать в процесс множество разнообразных критериев качества, что открывает двери для мультидисциплинарного применения.
Стоит отметить и оптимизацию затрат времени в процессе итеративного поиска. Полное количество шагов денойзинга можно значительно сократить на ранних стадиях, когда нужно лишь быстро отсортировать множество кандидатов по приблизительной оценке их качества. Только в финальных итерациях стоит выполнять более тщательное качественное моделирование с максимальным числом шагов. Такой подход ускоряет процесс и не жертвует окончательным результатом. Использование латентного пространства диффузионных моделей даёт ряд существенных преимуществ по сравнению с прямой оптимизацией в исходном, высокоразмерном пространстве объектов — латентное пространство обычно в несколько раз меньше по размеру и структурно организовано, что облегчает и ускоряет эффективный поиск.
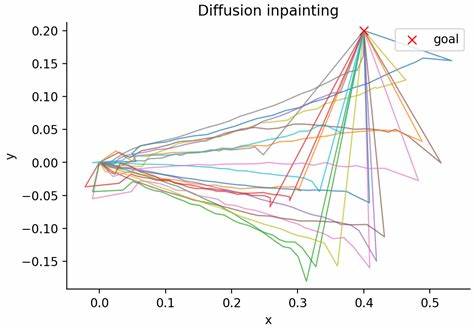
Кроме того, благодаря тому, что диффузионная модель фактически выучивает статистику и геометрию распределения данных, поиск в этом пространстве означает движение по реальному «многообразию данных», что позволяет избежать бессмысленных и недействительных вариантов, часто встречающихся при прямой оптимизации. При желании и по мере роста числа итераций можно усложнять модель латентного пространства — например, изначально используя простое гауссовское распределение, позднее можно перейти к смесям распределений или другим вероятностным моделям, что даст дополнительные возможности для более глубокого и комплексного исследования пространства решений. На практике методы Diffusion Elites показали впечатляющие результаты во множестве экспериментов и кейсов. Разработчик концепции приводил пример поиска траекторий робота на основе простейшей кинематической модели, где начальный датасет состоял из гладких дуг с вариативными параметрами движения. Благодаря Diffusion Elites за несколько итераций алгоритм быстро научился генерировать траектории, точно приближающиеся к заданной целевой позиции.
Такой подход гораздо эффективнее классического диффузионного заполнения (inpainting), который в подобных задачах нередко выдаёт ломаные и нереалистичные траектории, выходя за пределы правдоподобного многообразия. Именно здесь проявляется сила сочетания эволюционного поиска и диффузионного моделирования. Технология уже сегодня предоставляет значительный потенциал для применения в таких областях, как планирование поведения роботов, генерация новых молекул и материалов, дизайн сложных систем, а также там, где важна высокая эффективность поиска в сложных или высокоразмерных пространствах с жёсткими критериями оценки. С точки зрения разработчиков и исследователей, Diffusion Elites одинаково привлекателен благодаря своей простоте реализации и фундаментальной теоретической базе, подкреплённой десятками лет разработки методов перекрестной энтропии и эволюционных алгоритмов. Несложный псевдокод позволяет быстро стартовать с внедрением алгоритма, интегрировать его с любыми предобученными диффузионными моделями и адаптировать под конкретные прикладные задачи.