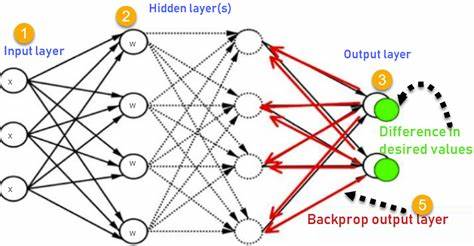
Обратное распространение ошибки, известное как backpropagation, является краеугольным камнем современного машинного обучения и основным механизмом обучения нейронных сетей. Этот алгоритм задаёт правила, с помощью которых нейронная сеть корректирует свои внутренние параметры — веса и смещения — чтобы лучше подстраиваться под заданные данные, минимизируя ошибки предсказаний. Несмотря на глубокую математическую составляющую, при детальном рассмотрении и упрощении понимания становится очевидна простота и элегантность метода. Основная задача любой нейронной сети — это поиск таких параметров, которые сводят к минимуму функцию потерь, измеряющую расхождение между предсказаниями модели и реальными значениями. Например, при решении задачи регрессии часто применяется среднеквадратическая ошибка.
Суть обратного распространения ошибки заключается в вычислении производных функции потерь по каждому параметру сети, чтобы определить направление, в котором необходимо изменить веса для уменьшения ошибки. Начинать освоение этого процесса полезно с простейшего случая — одной нейроной единицы без скрытых слоёв, где выход — линейная комбинация входного значения, веса и смещения. Можно представить себе ситуацию, где изменяя вес и смещение вручную, наблюдаешь за тем, как меняется ошибка, стремясь довести её до нуля. Такой интуитивный эксперимент помогает понять, что цель — сделать шаги в направлении уменьшения ошибки, а не случайно менять параметры. Чтобы формализовать этот процесс, нужна концепция градиента — вектор, который показывает направление наибольшего увеличения функции потерь.
Так как задача — свести ошибку к минимуму, используется направление, противоположное градиенту, называемое направлением наискорейшего спуска. Алгоритм градиентного спуска шаг за шагом перемещает параметры в сторону уменьшения ошибки. Ключевой проблемой является вычисление этих производных при многоуровневой структуре сети, где функция выходного значения представлена как сложное вложенное отображение. Тут на помощь приходит правило цепочки из математического анализа, которое позволяет рассчитывать производные сложных функций посредством последовательного умножения производных составляющих. Именно оно лежит в основе механизма обратного распространения ошибки.
Технически процесс начинается с вычисления ошибки и затем переходит к поэтапному вычислению производных относительно параметров, двигаясь назад по сети. Такое движение, обратное направлению вычисления выходных значений — отсюда и название «обратное» распространение. Чтобы закрепить теорию на практике, рассмотрим конкретный пример. Пусть имеется одна нейронная единица с весом, равным 1, и смещением 0. На вход подается значение 2.
1, а желаемый выход — 4. На первом шаге производится прямой проход, когда вычисляется предсказание на основе текущих параметров. Ошибка — это квадрат разницы между предсказанным и настоящим значением. Далее начинается обратное распространение, в ходе которого вычисляются частные производные функции потерь по весу и смещению. Эти значения показывают, насколько изменение каждого параметра влияет на ошибку.
После этого параметры корректируются с использованием вычисленных градиентов и заданной скорости обучения. В повторном прямом проходе видно, что ошибка уменьшилась — нейрон стал работать точнее. В реальных задачах основная сложность связана с глубиной и шириной нейронных сетей. Чтобы успешно моделировать нелинейные зависимости, сеть усложняют, вводя несколько скрытых слоев и применяя нелинейные функции активации, такие как ReLU. Эти функции позволяют нейрону либо активироваться, либо «выключаться», формируя тем самым нелинейные модели, которые гораздо лучше справляются с реальными данными.
Каждый такой слой — это новая вложенная функция, и обратное распространение применяется ко всем слоям последовательно, от выхода к входу, используя цепное правило для вычисления градиентов каждого параметра. Обучение глубокой нейронной сети сводится к многократному повторению итераций прямого и обратного проходов, каждый из которых вычисляет предсказания и корректирует параметры. На каждом шаге алгоритм использует накопленные значения производных, что делает процесс достаточно эффективным и позволяет адаптироваться даже к очень большим моделям. Визуализация обучающего процесса часто осуществляется с помощью контурных графиков, где изображены значения функции потерь в зависимости от параметров. Эти графики напоминают горы и долины, где цель — достичь самой низкой точки.
Обратное распространение вместе с градиентным спуском — это способ «спуститься в долину» с максимальной скоростью и избежать застревания на вершинах и ложных минимумах. Современные инструменты и библиотеки, такие как TensorFlow и PyTorch, автоматизируют вычисления обратного распространения с помощью автоматического дифференциирования, позволяя разработчикам сосредоточиться на архитектуре модели и данных. Но понимание базовых принципов помогает глубже понять, как и почему модель обучается. Обратное распространение — фундамент, на котором построены все современные методы глубокого обучения. Независимо от размера сети или сложности задачи, алгоритм остаётся неизменным в своей сути: вычислять градиенты и шагать навстречу уменьшению ошибки.
Это позволяет моделям адаптироваться и улучшать свои предсказания со временем, что лежит в основе искусственного интеллекта и его заявленного потенциала. Понимание обратного распространения открывает двери к эффективному проектированию и оптимизации нейронных сетей, даёт ясность в вопросах обучения и корректировки моделей и помогает взглянуть на сложные вычисления как на пошаговый и систематичный процесс настройки параметров. Благодаря этому алгоритму обучение становится не просто математической абстракцией, а реальным инструментом, делающим возможным интеллектуальную обработку данных во множестве прикладных областей — от распознавания образов и обработки речи до анализа текста и медицинской диагностики. Таким образом, обратное распространение — это не просто техника, а ключ к сознательному и контролируемому обучению нейросетей, который лежит в основе бесчисленных современных прорывов в сфере искусственного интеллекта и машинного обучения.