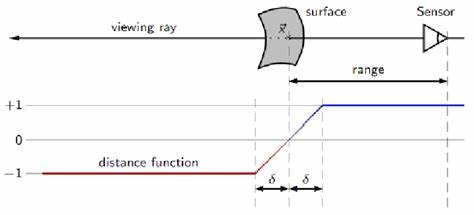
Антиалиасинг является одной из ключевых техник в компьютерной графике, направленной на сглаживание рваных краёв и улучшение качества визуального восприятия изображений. Несмотря на кажущуюся простоту этой задачи, совершенствование антиалиасинга остаётся сложной проблемой, особенно когда речь идёт о работе с подписанными функциями расстояния (Signed Distance Functions, SDF). Эти функции широко применяются благодаря их уникальным математическим свойствам, позволяющим точно описывать форму объектов и определять расстояние до их поверхности. Однако организация корректного и эффективного антиалиасинга на базе SDF требует глубокого понимания как теоретической, так и практической сторон вопроса. SDF — это функции, возвращающие подписанное расстояние от произвольной точки в пространстве до границы заданного объекта.
Положительное значение обычно означает, что точка находится внутри объекта, отрицательное — снаружи, а ноль указывает на саму границу. Такая постановка не только упрощает вычисления, но и обеспечивает уникальное преимущество: градиент на границах всегда имеет длину равную единице, что отражает линейный рост или спад функции вблизи контура. Именно эта особенность становится ключевой при реализации антиалиасинга. Основная идея антиалиасинга с применением SDF сводится к плавному переходу прозрачности (альфа-значения) между областью внутри объекта и фоном. Для этого используется длинна переходной зоны, условно называемой шириной размытости или диффузии, обозначаемой как w.
Она определяет, на каком пространственном промежутке вокруг границы объекта будет происходить постепенный переход от полной непрозрачности до полной прозрачности. Классический подход базируется на использовании функций типа linearstep — линейного интерполятора, резюмируемого формулой clаmp(0.5 + d/w, 0, 1), где d — текущее подписанное расстояние. Эта простая формула обеспечивает центрированный плавный переход в диапазоне от –w/2 до w/2, сохраняя максимальную простоту и эффективность вычислений. В зависимости от предпочтений можно сдвинуть переход на внутреннюю или внешнюю сторону контура, что позволяет контролировать визуальный эффект.
Тем не менее, не менее важным аспектом, влияющим на качество антиалиасинга, является выбор ширины w, которая, по сути, представляет собой размер пикселя, выраженный в координатах пространства, где осуществляется вычисление SDF. В двумерном мире при заданном размере изображения ширина w может быть вычислена на основе разрешения экрана, что гарантирует согласованность переходной зоны с физическим размером пикселя. Однако при работе с 3D-сценами, где объекты могут отображаться под разными углами и расстояниями, фиксированное значение ширины вызывает проблемы, проявляющиеся в неравномерном сглаживании поверхностей на переднем плане и заднем фоне. Для преодоления этих ограничений применяется использование численных производных — специальных функций, вычисляющих локальную скорость изменения подписанного расстояния на уровне фрагментов изображения. Так, функция fwidth(d), которая учитывает производные по обеим координатам (x и y), служит отличным динамическим параметром ширины перехода и автоматически адаптируется к перспективе и масштабированию объектов.
Этот прием позволяет достичь грамотного и ровного антиалиасинга по всей области изображения независимо от её трансформаций. Помимо калькуляции ширины диффузии, важным моментом является выбор формы кривой перехода. Вместо громоздкого smoothstep, иногда применяют linearstep, который теоретически быстрее и проще. Однако эксперименты показывают, что использование smoothstep более предпочтительно с эстетической точки зрения: плавное сглаживание с использованием гладкой кубической функции избавляет от зрительных артефактов и неприятных переходов, делая контуры гораздо более естественными для восприятия. Более продвинутые функции с ещё большей плавностью, такие как smootherstep, построенные на основе квинтической полиномиальной интерполяции, обеспечивают ещё более мягкое и приятное глазу отображение краёв.
Не стоит забывать и о цветовом пространстве, где происходит смешивание цвета фоновой и объектной областей с учётом вычисленной прозрачности. Обычно при антиалиасинге достаточно линейного смешивания цветов, что соответствует простому интерполяционному подходу. Однако для более точного и воспринимаемого глазами результата предпочтительнее использовать более совершенные цветовые представления, например, OkLab, которые учитывают особенности человеческого зрения и создают более гармоничные переходы, особенно при работе с размытием и полупрозрачностью. Таким образом, совершенствование антиалиасинга на основе подписанных функций расстояния становится вопросом комплексного подхода, где учитываются особенности вычисления расстояний, корректный выбор ширины перехода, адаптация к пространственным трансформациям и перспектива, выбор формы интерполяционной функции и правильная цветовая обработка. Простота формулы антиалиасинга здесь выступает в роли маскирующей иллюзии, за которой скрываются множество нюансов и тонкостей, выявленных в ходе экспериментов и анализов.
Современные компьютерные графические движки и инструменты активно используют данный метод для прорисовки криволинейных объектов с минимальными затратами ресурсов и максимальной визуальной чёткостью. Применение SDF с продвинутым антиалиасингом крайне важно для создания качественной визуализации в играх, при моделировании шрифтов, в системах рендеринга текстур, а также в VR и AR решениях, где затраты на производительность критически значимы. Благодаря развитию вычислительных мощностей и появлению более универсальных API в графических процессорах, стало возможным легко внедрять адаптивные вычисления, использующие численные производные. Это справедливо как для статичных 2D изображений, так и для сложных 3D сцен с динамическими освещениями и перемещениями камер. В конечном итоге, антиалиасинг на базе подписанных функций расстояния является одним из самых элегантных и эффективных решений в современном поле компьютерной графики.