Импульсные нейронные сети (Spiking Neural Networks, SNN) — это биологически вдохновленный подход в области искусственного интеллекта, который имитирует работу нейронов живого мозга. Такие сети отличаются тем, что передача информации происходит в виде дискретных импульсов — спайков, что позволяет моделировать временные и динамические процессы более естественно по сравнению с традиционными нейронными сетями. В последние годы импульсные сети приобретают всё большую популярность благодаря потенциалу энергоэффективных вычислений и улучшенной биологической интерпретируемости. В данной статье рассмотрим, как создать импульсную нейронную сеть для классификации рукописных цифр из набора данных MNIST, используя исключительно Python и библиотеку numpy, при этом PyTorch будет применён только для загрузки данных. Такой подход раскрывает глубокий смысл внутренней механики работы SNN и обучения с суррогатными градиентами с помощью обратного распространения ошибки во времени (BPTT).
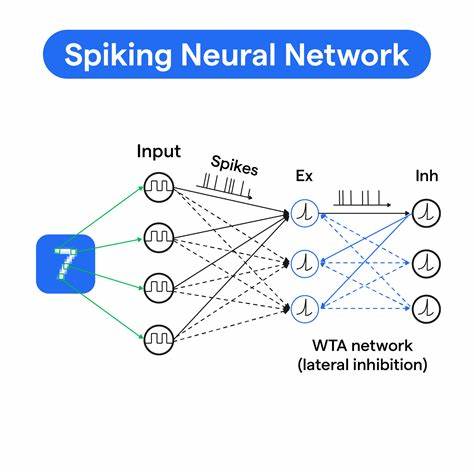
MNIST — это широко используемый в исследованиях по машинному обучению датасет, содержащий 70 000 изображений рукописных цифр размером 28х28 пикселей. Для работы с импульсными нейронными сетями, которые обрабатывают временные последовательности, статичное изображение необходимо корректно преобразовать в форму временного ряда. Для этого применяется вероятностное кодирование с помощью Пуассоновских процессов, в результате чего каждый пиксель изображения превращается в последовательность спайков, интенсивность которых пропорциональна яркости пикселя. Такое кодирование создаёт бинарные последовательности сигналов, которые подаются на вход сети в каждом временном шаге. Архитектура построенной сети состоит из трёх основных слоёв: входного слоя с 784 нейронами (по одному на каждый пиксель изображения), скрытого слоя из 100 нейронов и выходного слоя с 10 нейронами, соответствующими классам цифр от 0 до 9.
Все нейроны реализованы по принципу гидроподобных моделей утечек с интеграцией и генерацией спайка – так называемых leaky integrate-and-fire (LIF) нейронов. Поведение мембранного потенциала нейрона описывается дифференциальным уравнением, которое дискретизируется в вычислительном процессе и определяет накопление входных импульсов с коэффициентом утечки и последующим сбросом потенциала при достижении порога возбуждения. Модель обучается с использованием алгоритма обратного распространения ошибки сквозь время с суррогатными градиентами. Обычный механизм обратного распространения в традиционных нейронных сетях не подходит напрямую для SNN из‑за дискретной искажающей производные функции активации в виде спайков (шаговой функции), которая не является дифференцируемой. Для решения этой проблемы была использована идея суррогатных градиентов: во время обратного прохода дискретная функция аппроксимируется гладкой сигмоидной функцией, что позволяет вычислять градиенты для обновления весовых коэффициентов сети.
В процессе прямого прохода на каждом временном шаге входные сигналы представлены бинарным массивом спайков, через который активируются скрытые нейроны, а затем выходные. Мембранный потенциал нейронов обновляется по формуле с коэффициентом утечки (альфа), а при превышении порога (в нашем случае 0.6 единиц) генерируется спайк и мембранный потенциал сбрасывается до нуля. Данные активности и значения суррогатных градиентов сохраняются для последующего этапа BPTT. Функция потерь реализована с помощью кросс-энтропии между классами, где учитывается суммарная активность спайков выходных нейронов за всю длительность подачи входного сигнала (100 временных шагов).
Такой подход известен как rate coding, где количество сгенерированных спайков отражает вероятность принадлежности к определённому классу. В результате обучение с помощью градиентного спуска позволяет постепенно минимизировать функцию потерь и улучшать точность классификации. Особенностью обучения импульсных нейронных сетей является необходимость управления сложной динамикой временных зависимостей мембранных потенциалов и спайков, что осуществляется с помощью хранения истории активности нейронов и градиентов для каждого временного шага. Именно благодаря механизму BPTT вычисляемые градиенты корректно распределяются во времени, позволяя модели учитывать как непосредственное влияние входных сигналов, так и последовательные эффекты прошлых состояний. Обучение сеть осуществляется в мини-батчах размером 128 с количеством эпох до 10.
Во время тренировки сеть демонстрирует впечатляющую эффективность, достигая около 94% точности на тестовом наборе MNIST всего за 5 эпох, что подтверждает потенциал импульсных сетей в задачах распознавания образов. Код модели основан на библиотеке numpy и может запускаться на обычных CPU без необходимости дорогостоящих графических ускорителей, что подчёркивает доступность такого подхода для исследователей, изучающих биологические механизмы нейронной обработки и альтернативные вычислительные модели. Для того чтобы углубиться в технические детали, стоит подчеркнуть важность нескольких ключевых компонентов. Во-первых, коэффициент утечки α (обычно 0.95) определяет скорость затухания мембранного потенциала, влияя на кратковременную память нейронов.
Во-вторых, суррогатная функция с параметром steepness β формирует гладкий переход вблизи порога для вычисления производных, позволяя сохранить высокую точность обучения при учёте дискретного характера спайков. В-третьих, применение кросс-энтропийной функции потерь обеспечивает совместимость с классической теорией вероятностей, адаптируя её под spiking-архитектуру. На этапе обратного прохода значения локальных градиентов ошибок плавно распространяются сквозь время, начиная с последнего временного шага к первому. Внутри каждого временного шага реализуется подсчёт вкладов в градиенты весов между слоями с учётом суррогатных градиентов и накопленных вкладах предыдущих шагов, что обеспечивает устойчивое и эффективное обучение. Для предотвращения чрезмерного роста градиентов используется обрезка значений, поддерживающая численную стабильность.
Визуализация результатов обучения демонстрирует, как со временем распределение весов сети трансформируется из случайного в более структурированное, отражая способность сети выявлять значимые паттерны во входных данных. Особое внимание уделяется динамикам активности нейронов — как мембранные потенциалы скрытого и выходного слоёв изменяются в зависимости от поступающих входных сигналов и генерируемых спайков. Эти наблюдения помогают лучше понять внутренний механизм классификации, свойственный spiking-нейронным сетям. Разработка и обучение SNN при помощи исключительно numpy подчеркивает пользу экспериментального подхода без использования высокоуровневых нейросетевых фреймворков. Это позволяет глубоко углубиться в каждый этап вычислений, объясняя и формализуя процессы обновления потенциалов, вычисления градиентов и корректировки весов.
При этом подход остаётся масштабируемым — архитектуру легко адаптировать для других похожих задач, например, для классификации изображений из датасета FashionMNIST. Таким образом, импульсные нейронные сети представляют собой перспективную область исследований в искусственном интеллекте, сочетая биологическую правдоподобность с эффективными методами обучения. Их применение для задач классификации изображений, таких как MNIST, подтверждает практическую ценность. Модели SNN не только позволяют изучать динамические процессы в нейронах, но и способствуют развитию энергоэффективных вычислительных систем с потенциалом реализации на специализированном аппаратном обеспечении. Для желающих подробно изучить реализацию и понять вычислительные нюансы, доступен открытый репозиторий проекта на GitHub.
Он содержит полный исходный код с комментариями и наглядными примерами работы сети над MNIST. Этот ресурс служит прекрасным учебным материалом для студентов и исследователей, желающих освоить современные технологии импульсного машинного обучения и внести свой вклад в развитие области. В заключение можно отметить, что обучение импульсных нейронных сетей с использованием суррогатных градиентов и BPTT открывает новые горизонты в понимании и применении нейроподобных моделей. Такая методология позволяет не только строить эффективные классификаторы изображений, но и способствует созданию когнитивных машин с человеческими способностями восприятия и обучения, приближая искусственный интеллект к уровню живых организмов.