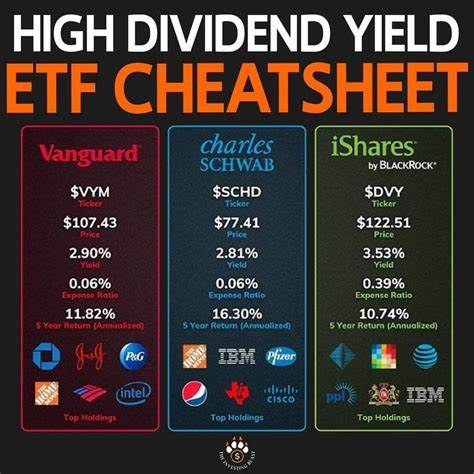
Оценка активов — одна из ключевых задач инвестора, которая напрямую влияет на принятие решений и размер потенциальной прибыли. При этом волатильность актива, то есть степень колебания его доходности, играет решающую роль в формировании цены и риске н вложений. Интуитивно может показаться, что чем выше ожидаемая доходность, тем дороже актив, однако высокая волатильность часто сопровождается большими рисками, что влияет на конечную стоимость бизнеса или инвестиции. Рассмотрим детально, как учитывать разные уровни волатильности при оценке активов и почему простой подход «доходность умножить на коэффициент» далеко не всегда подходит. В основе традиционной оценки лежит понятие дисконтированных денежных потоков.
Этот метод предполагает прогнозирование денежных поступлений от актива и их пересчет в текущую стоимость с использованием ставки дисконтирования, отражающей альтернативные возможности вложений и уровень риска. Для безрискового дохода, например, облигаций правительства со стабильной выплатой купонов, ставка дисконтирования берется на основе безрисковой процентной ставки, которую можно получить в банке или на рынке. Если будущий доход известен точно, цена актива равна сумме его будущих поступлений, дисконтированных по безрисковой ставке. В такой ситуации цена определяется формулой, представляющей собой сумму ряда с учетом ставки дисконтирования. При постоянном доходе она упрощается до деления годового дохода на ставку дисконтирования.
С ростом процентных ставок стоимость актива падает и наоборот. Это классический финансовый подход, применим далеко не ко всем инвестициям. Реальный бизнес и рынок акций характеризуются неопределённостью, и доходы компании могут колебаться. Здесь на первый план выходит волатильность — измеритель разброса доходности. Простейшая модель распределения дохода — нормальное распределение, но оно не подходит для описания доходности активов, так как предполагает возможность потерь сверх 100%, что невозможно.
Более реалистичной считается модель логнормального распределения, где доходность выражается в процентах и никогда не бывает меньше -100%. Суть различия лежит в отношении между арифметической средней доходностью и геометрической средней доходностью. Арифметическая средняя отражает математическое ожидание дохода за период, не учитывая влияние накопления дохода и рисков потерь, тогда как геометрическая средняя учитывает сложный процент и риск, показывая реальную среднегодовую доходность за длительный срок. Геометрическая средняя всегда ниже арифметической, особенно при высокой волатильности, что связано с тем, что нестабильность доходов уменьшает конечный итог вложений из-за эффекта просадки и восстановления. В языке формул это означает, что если средний арифметический доход равен μа, а стандартное отклонение доходности σ, то средний геометрический доход μ связан с ними соотношением μ=μа−σ2/2.
Это явление следует из неравенства Дженсена и отражает фундаментальное ограничение для инвесторов: высокая волатильность снижает эффективный рост капитала. На примере реальных данных американского рынка акций видно, что логнормальное распределение и эта формула хорошо описывают исторические результаты и показывают адекватное снижение доходности при росте риска. Исходя из этого, оценка будущих денежных потоков должна учитывать не столько среднее арифметическое значение дохода, сколько уменьшенный с поправкой на волатильность рост. Если пренебречь риском, то можно переоценить стоимость актива и, как следствие, понести убытки. Следующий важный аспект — возможность использования рычага (кредита) для увеличения потенциальной доходности.
Теоретически можно увеличить доходность и риски пропорционально кредитному плечу, но оптимальный уровень заимствования регулируется соотношением арифметической доходности, ставки заимствования и дисперсии доходности. Максимизируя геометрический рост капитала, инвестор может подобрать идеальный коэффициент рычага, известный как формула Келли, который позволяет избегать чрезмерных потерь от высокой волатильности и одновременно использовать благоприятные возможности. При формировании инвестиционного портфеля на практике приходится учитывать не один актив, а совокупность ценных бумаг с разными уровнями доходности, риска и взаимной корреляцией. Корреляция между активами влияет на совокупный риск портфеля: инвестируя в не полностью коррелированные активы, можно значительно снизить общий риск при сохранении доходности, тем самым увеличивая эффективную геометрическую доходность. Математически это выражается в формуле, включающей вектор распределения капитала между активами, вектор их доходностей и матрицу ковариаций.